备考浙教版中考数学题型专项训练 数与式解答题专练
教材版本:数学
试卷分类:数学中考
试卷大小:1.0 MB
文件类型:.doc 或 .pdf 或 .zip
发布时间:2024-05-01
授权方式:免费下载
下载地址:点此下载
以下为试卷部分试题预览
| 1. 综合题 | |
|
观察以下等式:
第1个等式: 第2个等式: 第3个等式: 第4个等式: 第5个等式: …… 按照以上规律,解决下列问题:
|
|
| 2. 综合题 | |
|
观察以下等式:
第一个等式: 第二个等式: 第三个等式: … 按照上述规律,解决下列问题:
|
|
| 3. 综合题 | |
|
阅读理解:对于任意一个四位数,若千位数字与十位数字均为奇数,百位数字与个位数字均为偶数,则称这个四位数为“均衡数”.将一个“均衡数”的千位数字与十位数字组成一个新的两位数m,原来千位数字作为m的十位数字;将一个“均衡数”的百位数字与个位数字组成另一个新的两位数n,原来百位数字作为n的十位数字.例如:“均衡数”3812,则
 .若 .若 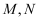 各个数位上的数字都不为零且十位数字大于个位数字,则将m中的任意一个数字作为一个新的两位数的十位数字,n中的任意一个数字作为这个新的两位数的个位数字,按这个方式产生的所有新的两位数的和记为 各个数位上的数字都不为零且十位数字大于个位数字,则将m中的任意一个数字作为一个新的两位数的十位数字,n中的任意一个数字作为这个新的两位数的个位数字,按这个方式产生的所有新的两位数的和记为  .例如: .例如:  时, 时,  . .
|
|
| 4. 综合题 | |
|
“字母表示数”的系统化阐述是由16世纪法国数学家韦达提出的,被后人称为从“算术”到“代数”的一次飞跃,从而大大推动了数学的发展.经过初中三年数学的学习,我们知道了用字母表示数可以分析从特殊到一般的数学规律,字母与数一样,也可以参与运算.请同学们观察下列等式:
第1个等式: 第2个等式: 第3个等式: 第4个等式: 第5个等式: …… 按照以上规律,解答下列问题:
|
|
| 5. 综合题 | |
|
对于二次函数
 和一次函数 和一次函数  ,我们把 ,我们把  称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务: 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(尝试)
|
|
| 6. 综合题 | |
|
对于四个数“-8,-2,1,3”及四种运算“+,-,×,÷”,列算式解答:
|
|
| 7. 综合题 | |
|
阅读材料:
《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂,从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法. 例如:已知 解:原式 问题解决:
|
|
| 8. 综合题 | |
|
材料一:对于一个四位数
 , 若满足千位数字与十位数字的和等于百位数字与个位数字的和,则称这个数为“间位等和数”,例如: , 若满足千位数字与十位数字的和等于百位数字与个位数字的和,则称这个数为“间位等和数”,例如:
材料二:将一个四位数
|
|
| 9. 综合题 | |
|
在平面直角坐标系
 中,对于任意两点 中,对于任意两点  , , 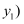 与 与  , ,  的“非常距离”,给出如下定义: 的“非常距离”,给出如下定义:
若 若 例如:点
|
|
| 10. 综合题 | |
|
阅读材料:在处理分数和分式的问题时,有时由于分子大于分母,或分子的次数高于分母的次数,在实际运算时难度较大,这时,我们可将分数(分式)拆分成一个整数(整式)与一个真分数(真分式)的和(差)的形式,通过对它的简单分析来解决问题,我们称这种方法为分离常数法,此法在处理分式或整除问题时颇为有效.
将分式分离常数可类比假分数变形带分数的方法进行,如: 根据以上阅读材料,解答下列问题:
|
|
- 广西百色市2020年数学中考模拟试卷(二)
- 华师大版数学八年级下册第二十章第一节20.1.1平均数的意义同步练习
- 初中数学华师大版八年级上学期 第14章测试卷
- 初中数学浙教版八年级上册2.5 逆命题和逆定理同步练习
- 湖北省黄石市下陆区2018-2019学年七年级上学期数学期末考试试卷
- 2016年四川省宜宾市中考数学试卷
- 初中数学浙教版八年级上册4.3 坐标平面内图形的轴对称和平移 同步练习
- 浙江省金华市2018-2019学年九年级上学期数学期中考试试卷
- 湖南省岳阳市华容县2019-2020学年八年级下学期数学期末考试试卷
- 四川省眉山市2020年中考数学试卷
- 四川省泸州市泸县2019-2020学年七年级下学期数学期末试卷
- 北京市大兴区2018-2019学年八年级下学期数学期末考试试卷
 =1,
=1, ,
, ,
, ,
, ,
,


 ;
; ;
; ;
; ;
; ;
; ,且
,且  ,求正整数
,求正整数  的值.
的值.
 的顶点坐标为
的顶点坐标为
 是二次函数
是二次函数 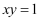 ,求
,求  的值.
的值. .
. 的值为 ▲ ;
的值为 ▲ ; .
. ,求
,求  的值.
的值.
 , ∵
, ∵ , ∴5247是“间位等和数”;
, ∴5247是“间位等和数”; , ∵
, ∵ , ∴3145不是“间位等和数”
, ∴3145不是“间位等和数” , 记
, 记 .例如
.例如 .
. 和
和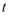 都是“间位等和数”,其中
都是“间位等和数”,其中 ,
,  (
( ,
,  ,
,  ,
,  且
且 ,
,  ,
, 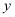 均为整数),规定:
均为整数),规定: , 若
, 若 , 求
, 求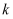 的最小值.
的最小值.
 ,则点
,则点  与点
与点 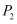 的“非常距离”为
的“非常距离”为  ;
; ,则点
,则点  .
. ,点
,点  ,因为
,因为  ,所以点
,所以点  ,也就是图1中线段
,也就是图1中线段  与线段
与线段  长度的较大值(点
长度的较大值(点 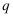 为垂直于
为垂直于  ,
,  ,
,  是直线
是直线  上的一个动点,
上的一个动点,
 的坐标是
的坐标是 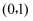 ,求点
,求点  是以原点
是以原点  为圆心,1为半径的圆上的一个动点,求点
为圆心,1为半径的圆上的一个动点,求点 
 ,这样,分式就拆分成一个分式
,这样,分式就拆分成一个分式 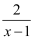 与一个整式
与一个整式 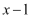 的和的形式.
的和的形式. 为负整数,可求得 x最大值= ;
为负整数,可求得 x最大值= ;
 的取值范围;
的取值范围;
 拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:
拆分成一个整式与一个真分式(分子为整数)的和(差)的形式为:  (整式部分对应等于
(整式部分对应等于  ,真分式部分对应等于
,真分式部分对应等于  ).
).
 有无最小值?如有,最小值为多少?
有无最小值?如有,最小值为多少?


