高中 数学
口袋中有形状和大小完全相同的五个球,编号分别为1,2,3,4,5,若从中一次随机摸出两个球,则摸出的两个球的编号之和大于6的概率为.
若不等式  的解集是
的解集是 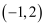 ,则下列选项正确的是( )
,则下列选项正确的是( )
 的解集是
的解集是 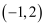 ,则下列选项正确的是( )
,则下列选项正确的是( )
A . 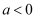 B .
B . 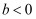 且
且 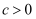 C .
C . 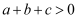 D . 不等式
D . 不等式  的解集是
的解集是 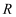
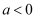 B .
B . 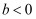 且
且 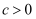 C .
C . 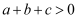 D . 不等式
D . 不等式  的解集是
的解集是 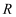
曲线  在点
在点  处的切线方程为( )
处的切线方程为( )
 在点
在点  处的切线方程为( )
处的切线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为(2  ,
,  ),曲线C的参数方程为
),曲线C的参数方程为  (α为参数).
(α为参数).
 ,
,  ),曲线C的参数方程为
),曲线C的参数方程为  (α为参数).
(α为参数).
-
(1) 直线l过M且与曲线C相切,求直线l的极坐标方程;
-
(2) 点N与点M关于y轴对称,求曲线C上的点到点N的距离的取值范围.
已知函数 

-
(1) 求函数
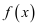 的单调递减区间;
的单调递减区间;
-
(2) 将函数
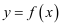 的图像向左平移
的图像向左平移  个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的  倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 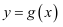 的图像,求
的图像,求 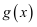 在
在  上的值域.
上的值域.
函数 的图像大致是( )
的图像大致是( )
 的图像大致是( )
的图像大致是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
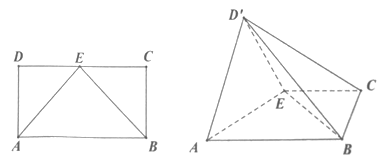
如图,在长方  中,
中, 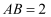 ,
, 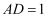 ,E为
,E为 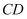 的中点,以
的中点,以 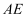 为折痕,把
为折痕,把 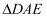 折起到
折起到  的位置,且平面
的位置,且平面  平面
平面  .
.
 中,
中, 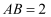 ,
, 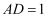 ,E为
,E为 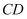 的中点,以
的中点,以 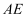 为折痕,把
为折痕,把 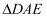 折起到
折起到  的位置,且平面
的位置,且平面  平面
平面  .
. 
-
(1) 求证:
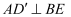 ;
;
-
(2) 在棱
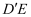 上是否存在一点P,使得
上是否存在一点P,使得 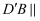 平面
平面  ,若存在,求出点P的位置,若不存在,请说明理由.
,若存在,求出点P的位置,若不存在,请说明理由.
现有三本相同的语文书和一本数学书,分发给三个学生,每个学生至少分得一本,问这样的分法有( )种.
A . 36
B . 9
C . 18
D . 15
等比数列  中,
中,  是表示其前项和,已知
是表示其前项和,已知 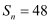 ,
,  ,则
,则  等于( )
等于( )
 中,
中,  是表示其前项和,已知
是表示其前项和,已知 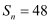 ,
,  ,则
,则  等于( )
等于( )
A . 183
B . 108
C . 75
D . 63
已知集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设  ,则( )
,则( )
 ,则( )
,则( )
A .  B .
B . 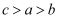 C .
C . 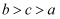 D .
D . 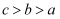
 B .
B . 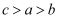 C .
C . 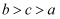 D .
D . 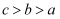
已知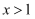 , 则
, 则 的最小值是;
的最小值是;
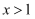 , 则
, 则 的最小值是;
的最小值是;
已知函数  ,
,  ,则该函数的值域为.
,则该函数的值域为.
 ,
,  ,则该函数的值域为.
,则该函数的值域为.
已知集合  ,
,  ,则
,则 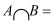 ( )
( )
 ,
,  ,则
,则 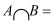 ( )
( )
A . 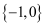 B .
B . 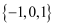 C .
C .  D .
D . 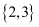
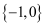 B .
B . 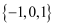 C .
C .  D .
D . 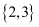
在 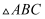 中,角
中,角 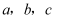 的对边分别为
的对边分别为 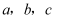 ,已知
,已知  .
.
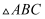 中,角
中,角 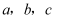 的对边分别为
的对边分别为 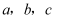 ,已知
,已知  .
.
-
(1) 求角
 的大小;
的大小;
-
(2) 若
 ,求
,求 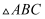 的面积.
的面积.
设A是自然数集的一个非空子集,对于 ,如果
,如果 ,且
,且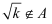 ,那么k是A的一个“酷元”,给定
,那么k是A的一个“酷元”,给定 ,设
,设 ,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )个
,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )个
 ,如果
,如果 ,且
,且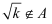 ,那么k是A的一个“酷元”,给定
,那么k是A的一个“酷元”,给定 ,设
,设 ,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )个
,且集合M中的两个元素都是“酷元”,那么这样的集合M有( )个
A . 3
B . 4
C . 5
D . 6
如图,在长方体  ,中,
,中,  ,
,  ,
,  、
、  、
、  分别是
分别是  ,
,  ,
, 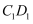 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( )
 ,中,
,中,  ,
,  ,
,  、
、  、
、  分别是
分别是  ,
,  ,
, 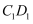 的中点,则下列说法正确的是( )
的中点,则下列说法正确的是( ) 
A . 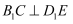 B .
B .  平面
平面  C . 若点P在平面ABCD内,且
C . 若点P在平面ABCD内,且  平面GEF,则线段
平面GEF,则线段  长度的最小值为
长度的最小值为  D . 若点Q在平面ABCD内,且
D . 若点Q在平面ABCD内,且 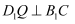 ,则线段
,则线段 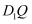 长度的最小值为
长度的最小值为 
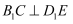 B .
B .  平面
平面  C . 若点P在平面ABCD内,且
C . 若点P在平面ABCD内,且  平面GEF,则线段
平面GEF,则线段  长度的最小值为
长度的最小值为  D . 若点Q在平面ABCD内,且
D . 若点Q在平面ABCD内,且 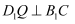 ,则线段
,则线段 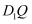 长度的最小值为
长度的最小值为 
等差数列 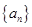 的首项
的首项  ,它的前
,它的前 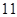 项的平均值为
项的平均值为  ,若从中抽去一项,余下的
,若从中抽去一项,余下的 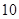 项的平均值为
项的平均值为 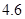 ,则抽去的是( )
,则抽去的是( )
A .  B .
B .  C .
C .  D .
D . 
已知矩形  中,
中, 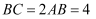 ,现向矩形
,现向矩形  内随机投掷质点
内随机投掷质点  ,则满足
,则满足  的概率是
的概率是 
 中,
中, 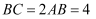 ,现向矩形
,现向矩形  内随机投掷质点
内随机投掷质点  ,则满足
,则满足  的概率是
的概率是 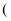
A . 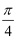 B .
B .  C .
C . 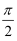 D .
D . 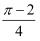
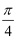 B .
B .  C .
C . 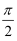 D .
D . 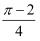
“双曲线C的方程为  (a>0,b>0)”是“双曲线C的渐近线方程为y=
(a>0,b>0)”是“双曲线C的渐近线方程为y=  ”的( )
”的( )
 (a>0,b>0)”是“双曲线C的渐近线方程为y=
(a>0,b>0)”是“双曲线C的渐近线方程为y=  ”的( )
”的( )
A . 充分非必要条件
B . 必要非充分条件
C . 充要条件
D . 既非充分又非必要条件
最近更新



