第дёҖз« з©әй—ҙеҗ‘йҮҸдёҺз«ӢдҪ“еҮ дҪ• зҹҘиҜҶзӮ№йўҳеә“
еҰӮеӣҫпјҢй•ҝж–№дҪ“ABCDп№ЈA1B1C1D1дёӯпјҢAA1=AB=2пјҢAD=1пјҢзӮ№EгҖҒFгҖҒGеҲҶеҲ«жҳҜDD1гҖҒABгҖҒCC1зҡ„дёӯзӮ№пјҢеҲҷејӮйқўзӣҙзәҝA1EдёҺGFжүҖжҲҗи§’зҡ„дҪҷејҰеҖјжҳҜпјҲгҖҖгҖҖпјү

A .  B .
B .  C .
C .  D . 0
D . 0
 B .
B .  C .
C .  D . 0
D . 0
гҖҠд№қз« з®—жңҜгҖӢдёӯпјҢе°Ҷеә•йқўдёәй•ҝж–№еҪўдё”жңүдёҖжқЎдҫ§жЈұдёҺеә•йқўеһӮзӣҙзҡ„еӣӣжЈұй”Ҙз§°д№Ӣдёәйҳій©¬пјҢе°ҶеӣӣдёӘйқўйғҪдёәзӣҙи§’дёүи§’еҪўзҡ„еӣӣйқўдҪ“з§°д№Ӣдёәйі–иҮ‘пјҺеҰӮеӣҫпјҢеңЁйҳій©¬Pп№ЈABCDдёӯпјҢдҫ§жЈұPDвҠҘеә•йқўABCDпјҢдё”PD=CDпјҢиҝҮжЈұPCзҡ„дёӯзӮ№EпјҢдҪңEFвҠҘPBдәӨPBдәҺзӮ№FпјҢиҝһжҺҘDEпјҢDFпјҢBDпјҢBEпјҺ

-
пјҲ1пјү иҜҒжҳҺпјҡPBвҠҘе№ійқўDEFпјҺиҜ•еҲӨж–ӯеӣӣйқўдҪ“DBEFжҳҜеҗҰдёәйі–иҮ‘пјҢиӢҘжҳҜпјҢеҶҷеҮәе…¶жҜҸдёӘйқўзҡ„зӣҙи§’пјҲеҸӘйңҖеҶҷеҮәз»“и®әпјүпјӣиӢҘдёҚжҳҜпјҢиҜҙжҳҺзҗҶз”ұпјӣ
-
пјҲ2пјү иӢҘйқўDEFдёҺйқўABCDжүҖжҲҗдәҢйқўи§’зҡ„еӨ§е°Ҹдёә
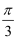 пјҢжұӮ
пјҢжұӮ  зҡ„еҖјпјҺ
зҡ„еҖјпјҺ
е·ІзҹҘзҗғ  зҡ„иЎЁйқўдёҠдёүзӮ№
зҡ„иЎЁйқўдёҠдёүзӮ№  гҖҒ
гҖҒ  гҖҒ
гҖҒ  ж»Ўи¶іпјҡ
ж»Ўи¶іпјҡ 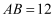 пјҢ
пјҢ 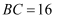 пјҢ
пјҢ 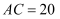 пјҢдё”зҗғеҝғеҲ°иҜҘжҲӘйқўзҡ„и·қзҰ»дёәзҗғзҡ„еҚҠеҫ„зҡ„дёҖеҚҠпјҢеҲҷ
пјҢдё”зҗғеҝғеҲ°иҜҘжҲӘйқўзҡ„и·қзҰ»дёәзҗғзҡ„еҚҠеҫ„зҡ„дёҖеҚҠпјҢеҲҷ  гҖҒ
гҖҒ  дёӨзӮ№зҡ„зҗғйқўи·қзҰ»жҳҜ.
дёӨзӮ№зҡ„зҗғйқўи·қзҰ»жҳҜ.
 зҡ„иЎЁйқўдёҠдёүзӮ№
зҡ„иЎЁйқўдёҠдёүзӮ№  гҖҒ
гҖҒ  гҖҒ
гҖҒ  ж»Ўи¶іпјҡ
ж»Ўи¶іпјҡ 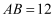 пјҢ
пјҢ 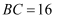 пјҢ
пјҢ 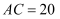 пјҢдё”зҗғеҝғеҲ°иҜҘжҲӘйқўзҡ„и·қзҰ»дёәзҗғзҡ„еҚҠеҫ„зҡ„дёҖеҚҠпјҢеҲҷ
пјҢдё”зҗғеҝғеҲ°иҜҘжҲӘйқўзҡ„и·қзҰ»дёәзҗғзҡ„еҚҠеҫ„зҡ„дёҖеҚҠпјҢеҲҷ  гҖҒ
гҖҒ  дёӨзӮ№зҡ„зҗғйқўи·қзҰ»жҳҜ.
дёӨзӮ№зҡ„зҗғйқўи·қзҰ»жҳҜ.
еңЁжўҜеҪў  дёӯпјҢ
дёӯпјҢ  пјҢ
пјҢ  дёә
дёә  зҡ„дёӯзӮ№пјҢзәҝж®ө
зҡ„дёӯзӮ№пјҢзәҝж®ө 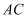 дёҺ
дёҺ 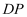 дәӨдәҺ
дәӨдәҺ  зӮ№пјҲеҰӮеӣҫ1пјү.е°Ҷ
зӮ№пјҲеҰӮеӣҫ1пјү.е°Ҷ 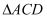 жІҝ
жІҝ 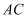 жҠҳиө·еҲ°
жҠҳиө·еҲ°  зҡ„дҪҚзҪ®пјҢдҪҝеҫ—дәҢйқўи§’
зҡ„дҪҚзҪ®пјҢдҪҝеҫ—дәҢйқўи§’  дёәзӣҙдәҢйқўи§’пјҲеҰӮеӣҫ2пјү.
дёәзӣҙдәҢйқўи§’пјҲеҰӮеӣҫ2пјү.
 дёӯпјҢ
дёӯпјҢ  пјҢ
пјҢ  дёә
дёә  зҡ„дёӯзӮ№пјҢзәҝж®ө
зҡ„дёӯзӮ№пјҢзәҝж®ө 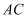 дёҺ
дёҺ 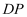 дәӨдәҺ
дәӨдәҺ  зӮ№пјҲеҰӮеӣҫ1пјү.е°Ҷ
зӮ№пјҲеҰӮеӣҫ1пјү.е°Ҷ 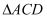 жІҝ
жІҝ 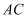 жҠҳиө·еҲ°
жҠҳиө·еҲ°  зҡ„дҪҚзҪ®пјҢдҪҝеҫ—дәҢйқўи§’
зҡ„дҪҚзҪ®пјҢдҪҝеҫ—дәҢйқўи§’  дёәзӣҙдәҢйқўи§’пјҲеҰӮеӣҫ2пјү.
дёәзӣҙдәҢйқўи§’пјҲеҰӮеӣҫ2пјү. 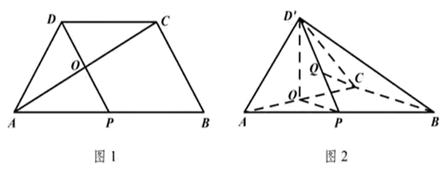
-
пјҲ1пјү жұӮиҜҒпјҡ
 е№ійқў
е№ійқў  пјӣ
пјӣ
-
пјҲ2пјү зәҝж®ө
 дёҠжҳҜеҗҰеӯҳеңЁзӮ№
дёҠжҳҜеҗҰеӯҳеңЁзӮ№ 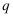 пјҢдҪҝеҫ—
пјҢдҪҝеҫ— 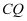 дёҺе№ійқў
дёҺе№ійқў  жүҖжҲҗи§’зҡ„жӯЈејҰеҖјдёә
жүҖжҲҗи§’зҡ„жӯЈејҰеҖјдёә  пјҹиӢҘеӯҳеңЁпјҢжұӮеҮә
пјҹиӢҘеӯҳеңЁпјҢжұӮеҮә  зҡ„еҖјпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұ.
зҡ„еҖјпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұ.
еҰӮеӣҫпјҢе·ІзҹҘе№ійқўеӣӣиҫ№еҪў  дёӯпјҢDдёә
дёӯпјҢDдёә 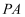 зҡ„дёӯзӮ№пјҢ
зҡ„дёӯзӮ№пјҢ  пјҢ
пјҢ 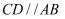 пјҢдё”
пјҢдё”  .е°ҶжӯӨе№ійқўеӣӣиҫ№еҪў
.е°ҶжӯӨе№ійқўеӣӣиҫ№еҪў  жІҝ
жІҝ 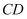 жҠҳиө·пјҢдё”е№ійқў
жҠҳиө·пјҢдё”е№ійқў  е№ійқў
е№ійқў  пјҢиҝһжҺҘ
пјҢиҝһжҺҘ 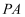 гҖҒ
гҖҒ  гҖҒ
гҖҒ 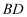 .
.
 дёӯпјҢDдёә
дёӯпјҢDдёә 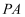 зҡ„дёӯзӮ№пјҢ
зҡ„дёӯзӮ№пјҢ  пјҢ
пјҢ 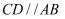 пјҢдё”
пјҢдё”  .е°ҶжӯӨе№ійқўеӣӣиҫ№еҪў
.е°ҶжӯӨе№ійқўеӣӣиҫ№еҪў  жІҝ
жІҝ 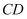 жҠҳиө·пјҢдё”е№ійқў
жҠҳиө·пјҢдё”е№ійқў  е№ійқў
е№ійқў  пјҢиҝһжҺҘ
пјҢиҝһжҺҘ 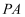 гҖҒ
гҖҒ  гҖҒ
гҖҒ 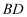 .
. 
пјҲв… пјүиҜҒжҳҺпјҡе№ійқў  е№ійқў
е№ійқў 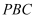 пјӣ
пјӣ
пјҲв…ЎпјүжұӮзӮ№  дёҺе№ійқў
дёҺе№ійқў 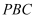 зҡ„и·қзҰ».
зҡ„и·қзҰ».
е·ІзҹҘеӣӣжЈұй”Ҙ 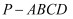 пјҢеә•йқў
пјҢеә•йқў  дёәиҸұеҪўпјҢ
дёәиҸұеҪўпјҢ  ,Hдёә
,Hдёә 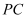 дёҠзҡ„зӮ№пјҢиҝҮ
дёҠзҡ„зӮ№пјҢиҝҮ 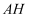 зҡ„е№ійқўеҲҶеҲ«дәӨ
зҡ„е№ійқўеҲҶеҲ«дәӨ  дәҺзӮ№
дәҺзӮ№ 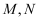 пјҢдё”
пјҢдё”  е№ійқў
е№ійқў  пјҺ
пјҺ
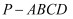 пјҢеә•йқў
пјҢеә•йқў  дёәиҸұеҪўпјҢ
дёәиҸұеҪўпјҢ  ,Hдёә
,Hдёә 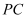 дёҠзҡ„зӮ№пјҢиҝҮ
дёҠзҡ„зӮ№пјҢиҝҮ 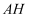 зҡ„е№ійқўеҲҶеҲ«дәӨ
зҡ„е№ійқўеҲҶеҲ«дәӨ  дәҺзӮ№
дәҺзӮ№ 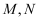 пјҢдё”
пјҢдё”  е№ійқў
е№ійқў  пјҺ
пјҺ 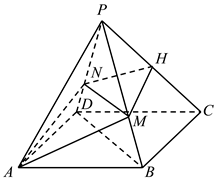
-
пјҲ1пјү иҜҒжҳҺпјҡ
 пјӣ
пјӣ
-
пјҲ2пјү еҪ“
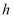 дёә
дёә 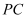 зҡ„дёӯзӮ№пјҢ
зҡ„дёӯзӮ№пјҢ  пјҢ
пјҢ 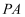 дёҺе№ійқў
дёҺе№ійқў  жүҖжҲҗзҡ„и§’дёә
жүҖжҲҗзҡ„и§’дёә 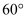 пјҢжұӮдәҢйқўи§’
пјҢжұӮдәҢйқўи§’  зҡ„дҪҷејҰеҖјпјҺ
зҡ„дҪҷејҰеҖјпјҺ
еҰӮеӣҫ  пјҢеңЁжўҜеҪў
пјҢеңЁжўҜеҪў  дёӯпјҢ
дёӯпјҢ 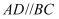 пјҢ
пјҢ  пјҢEдёә
пјҢEдёә 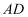 зҡ„дёӯзӮ№пјҢOжҳҜ
зҡ„дёӯзӮ№пјҢOжҳҜ 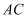 дёҺ
дёҺ 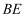 зҡ„дәӨзӮ№пјҢе°Ҷ
зҡ„дәӨзӮ№пјҢе°Ҷ  жІҝ
жІҝ 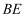 зҝ»жҠҳеҲ°еӣҫ2дёӯ
зҝ»жҠҳеҲ°еӣҫ2дёӯ  зҡ„дҪҚзҪ®пјҢеҫ—еҲ°еӣӣжЈұй”Ҙ
зҡ„дҪҚзҪ®пјҢеҫ—еҲ°еӣӣжЈұй”Ҙ 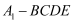 пјҺ
пјҺ
 пјҢеңЁжўҜеҪў
пјҢеңЁжўҜеҪў  дёӯпјҢ
дёӯпјҢ 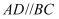 пјҢ
пјҢ  пјҢEдёә
пјҢEдёә 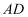 зҡ„дёӯзӮ№пјҢOжҳҜ
зҡ„дёӯзӮ№пјҢOжҳҜ 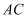 дёҺ
дёҺ 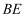 зҡ„дәӨзӮ№пјҢе°Ҷ
зҡ„дәӨзӮ№пјҢе°Ҷ  жІҝ
жІҝ 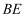 зҝ»жҠҳеҲ°еӣҫ2дёӯ
зҝ»жҠҳеҲ°еӣҫ2дёӯ  зҡ„дҪҚзҪ®пјҢеҫ—еҲ°еӣӣжЈұй”Ҙ
зҡ„дҪҚзҪ®пјҢеҫ—еҲ°еӣӣжЈұй”Ҙ  пјҺ
пјҺ 
-
пјҲ1пјү жұӮиҜҒпјҡ
 пјӣ
пјӣ
-
пјҲ2пјү еҪ“
 пјҢ
пјҢ  ж—¶пјҢжұӮ
ж—¶пјҢжұӮ  еҲ°е№ійқў
еҲ°е№ійқў  зҡ„и·қзҰ»пјҺ
зҡ„и·қзҰ»пјҺ
еңЁе№ійқўзӣҙи§’еқҗж Үзі»  дёӯпјҢзӮ№
дёӯпјҢзӮ№  зҡ„еқҗж Үдёә
зҡ„еқҗж Үдёә 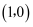 пјҢеңЁжһҒеқҗж Үзі»пјҲдёҺзӣҙи§’еқҗж Үзі»еҸ–зӣёеҗҢзҡ„й•ҝеәҰеҚ•дҪҚпјҢдё”д»ҘеҺҹзӮ№
пјҢеңЁжһҒеқҗж Үзі»пјҲдёҺзӣҙи§’еқҗж Үзі»еҸ–зӣёеҗҢзҡ„й•ҝеәҰеҚ•дҪҚпјҢдё”д»ҘеҺҹзӮ№  дёәжһҒзӮ№пјҢд»Ҙ
дёәжһҒзӮ№пјҢд»Ҙ  иҪҙжӯЈеҚҠиҪҙдёәжһҒиҪҙпјүдёӯпјҢзӣҙзәҝ
иҪҙжӯЈеҚҠиҪҙдёәжһҒиҪҙпјүдёӯпјҢзӣҙзәҝ  зҡ„ж–№зЁӢдёә
зҡ„ж–№зЁӢдёә  .
.
 дёӯпјҢзӮ№
дёӯпјҢзӮ№  зҡ„еқҗж Үдёә
зҡ„еқҗж Үдёә 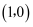 пјҢеңЁжһҒеқҗж Үзі»пјҲдёҺзӣҙи§’еқҗж Үзі»еҸ–зӣёеҗҢзҡ„й•ҝеәҰеҚ•дҪҚпјҢдё”д»ҘеҺҹзӮ№
пјҢеңЁжһҒеқҗж Үзі»пјҲдёҺзӣҙи§’еқҗж Үзі»еҸ–зӣёеҗҢзҡ„й•ҝеәҰеҚ•дҪҚпјҢдё”д»ҘеҺҹзӮ№  дёәжһҒзӮ№пјҢд»Ҙ
дёәжһҒзӮ№пјҢд»Ҙ  иҪҙжӯЈеҚҠиҪҙдёәжһҒиҪҙпјүдёӯпјҢзӣҙзәҝ
иҪҙжӯЈеҚҠиҪҙдёәжһҒиҪҙпјүдёӯпјҢзӣҙзәҝ  зҡ„ж–№зЁӢдёә
зҡ„ж–№зЁӢдёә  .
.
-
пјҲ1пјү еҲӨж–ӯзӮ№
 дёҺзӣҙзәҝ
дёҺзӣҙзәҝ  зҡ„дҪҚзҪ®е…ізі»пјӣ
зҡ„дҪҚзҪ®е…ізі»пјӣ
-
пјҲ2пјү и®ҫзӣҙзәҝ
 дёҺжӣІзәҝ
дёҺжӣІзәҝ  пјҲ
пјҲ 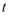 дёәеҸӮж•°пјҢ
дёәеҸӮж•°пјҢ  пјүзӣёдәӨдәҺ
пјүзӣёдәӨдәҺ  пјҢ
пјҢ  дёӨзӮ№пјҢжұӮзӮ№
дёӨзӮ№пјҢжұӮзӮ№  еҲ°
еҲ°  пјҢ
пјҢ  дёӨзӮ№зҡ„и·қзҰ»д№Ӣз§Ҝ.
дёӨзӮ№зҡ„и·қзҰ»д№Ӣз§Ҝ.
еҰӮеӣҫпјҢеӣӣжЈұй”Ҙ 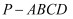 пјҢеӣӣиҫ№еҪў
пјҢеӣӣиҫ№еҪў  дёәе№іиЎҢеӣӣиҫ№еҪўпјҢ
дёәе№іиЎҢеӣӣиҫ№еҪўпјҢ 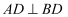 пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 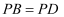 пјҢ
пјҢ  пјҢ
пјҢ  дёә
дёә  дёӯзӮ№.
дёӯзӮ№.
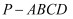 пјҢеӣӣиҫ№еҪў
пјҢеӣӣиҫ№еҪў  дёәе№іиЎҢеӣӣиҫ№еҪўпјҢ
дёәе№іиЎҢеӣӣиҫ№еҪўпјҢ 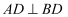 пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 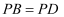 пјҢ
пјҢ  пјҢ
пјҢ  дёә
дёә  дёӯзӮ№.
дёӯзӮ№. 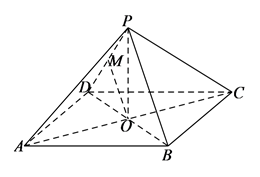
-
пјҲ1пјү жұӮиҜҒпјҡ
 е№ійқў
е№ійқў  пјӣ
пјӣ
-
пјҲ2пјү жұӮиҜҒпјҡе№ійқў
 е№ійқў
е№ійқў  пјӣ
пјӣ
-
пјҲ3пјү жұӮдәҢйқўи§’
 зҡ„дҪҷејҰеҖј.
зҡ„дҪҷејҰеҖј.
еҰӮеӣҫпјҢеңЁеӣӣжЈұй”Ҙ 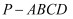 дёӯпјҢе·ІзҹҘеә•йқў
дёӯпјҢе·ІзҹҘеә•йқў  дёәзӯүи…°жўҜеҪўпјҢ
дёәзӯүи…°жўҜеҪўпјҢ 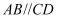 пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 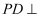 е№ійқў
е№ійқў  пјҢ
пјҢ  .
.
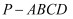 дёӯпјҢе·ІзҹҘеә•йқў
дёӯпјҢе·ІзҹҘеә•йқў  дёәзӯүи…°жўҜеҪўпјҢ
дёәзӯүи…°жўҜеҪўпјҢ 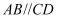 пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 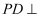 е№ійқў
е№ійқў  пјҢ
пјҢ  .
. 
-
пјҲ1пјү жұӮ
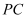 дёҺ
дёҺ 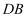 жүҖжҲҗи§’зҡ„дҪҷејҰеҖјпјӣ
жүҖжҲҗи§’зҡ„дҪҷејҰеҖјпјӣ
-
пјҲ2пјү и®ҫlжҳҜиҝҮзӮ№Pдё”дёҺ
 е№іиЎҢзҡ„дёҖжқЎзӣҙзәҝпјҢзӮ№QеңЁзӣҙзәҝlдёҠпјҢеҪ“
е№іиЎҢзҡ„дёҖжқЎзӣҙзәҝпјҢзӮ№QеңЁзӣҙзәҝlдёҠпјҢеҪ“ 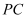 дёҺе№ійқў
дёҺе№ійқў  жүҖжҲҗи§’зҡ„жӯЈејҰеҖјжңҖеӨ§ж—¶пјҢжұӮзәҝж®ө
жүҖжҲҗи§’зҡ„жӯЈејҰеҖјжңҖеӨ§ж—¶пјҢжұӮзәҝж®ө  зҡ„й•ҝ.
зҡ„й•ҝ.
еҰӮеӣҫпјҢеңЁеӣӣжЈұй”Ҙ 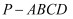 дёӯпјҢеә•йқў
дёӯпјҢеә•йқў  дёәжӯЈж–№еҪўпјҢдҫ§йқў
дёәжӯЈж–№еҪўпјҢдҫ§йқў 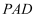 жҳҜжӯЈдёүи§’еҪўпјҢе№ійқў
жҳҜжӯЈдёүи§’еҪўпјҢе№ійқў  е№ійқў
е№ійқў  пјҢ
пјҢ  жҳҜ
жҳҜ  зҡ„дёӯзӮ№пјҺ
зҡ„дёӯзӮ№пјҺ
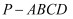 дёӯпјҢеә•йқў
дёӯпјҢеә•йқў  дёәжӯЈж–№еҪўпјҢдҫ§йқў
дёәжӯЈж–№еҪўпјҢдҫ§йқў 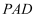 жҳҜжӯЈдёүи§’еҪўпјҢе№ійқў
жҳҜжӯЈдёүи§’еҪўпјҢе№ійқў  е№ійқў
е№ійқў  пјҢ
пјҢ  жҳҜ
жҳҜ  зҡ„дёӯзӮ№пјҺ
зҡ„дёӯзӮ№пјҺ 
-
пјҲ1пјү иҜҒжҳҺпјҡ
 е№ійқў
е№ійқў  пјӣ
пјӣ
-
пјҲ2пјү иӢҘ
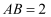 пјҢжұӮзӮ№
пјҢжұӮзӮ№  еҲ°е№ійқў
еҲ°е№ійқў 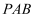 зҡ„и·қзҰ»пјҺ
зҡ„и·қзҰ»пјҺ
е·ІзҹҘеҗ‘йҮҸ  .
.
 .
.
-
пјҲ1пјү иӢҘ
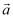 вҲҘ
вҲҘ 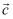 пјҢжұӮ
пјҢжұӮ  пјӣ
пјӣ
-
пјҲ2пјү иӢҘ
 пјҢжұӮ
пјҢжұӮ  зҡ„еҖј.
зҡ„еҖј.
еңЁй•ҝж–№дҪ“ дёӯпјҢ
дёӯпјҢ пјҢ
пјҢ  пјҢ зӮ№
пјҢ зӮ№ еңЁ
еңЁ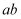 дёҠпјҢзӮ№
дёҠпјҢзӮ№ еңЁ
еңЁ дёҠпјҢ
дёҠпјҢ пјҢ еҲҷзӣҙзәҝ
пјҢ еҲҷзӣҙзәҝ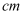 дёҺ
дёҺ жүҖжҲҗи§’зҡ„дҪҷејҰеҖјдёәпјҲ пјү
жүҖжҲҗи§’зҡ„дҪҷејҰеҖјдёәпјҲ пјү
 дёӯпјҢ
дёӯпјҢ пјҢ
пјҢ  пјҢ зӮ№
пјҢ зӮ№ еңЁ
еңЁ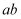 дёҠпјҢзӮ№
дёҠпјҢзӮ№ еңЁ
еңЁ дёҠпјҢ
дёҠпјҢ пјҢ еҲҷзӣҙзәҝ
пјҢ еҲҷзӣҙзәҝ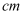 дёҺ
дёҺ жүҖжҲҗи§’зҡ„дҪҷејҰеҖјдёәпјҲ пјү
жүҖжҲҗи§’зҡ„дҪҷејҰеҖјдёәпјҲ пјү
A .  B .
B . 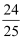 C .
C .  D .
D . 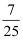
 B .
B . 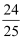 C .
C .  D .
D . 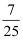
еҰӮеӣҫпјҢеңЁеӣӣжЈұй”Ҙ дёӯпјҢ
дёӯпјҢ пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 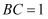 пјҢ
пјҢ  пјҢ
пјҢ 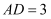 пјҢ
пјҢ 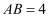 пјҢ
пјҢ  пјҺ
пјҺ
 дёӯпјҢ
дёӯпјҢ пјҢ
пјҢ  пјҢ
пјҢ  пјҢ
пјҢ 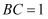 пјҢ
пјҢ  пјҢ
пјҢ 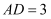 пјҢ
пјҢ 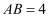 пјҢ
пјҢ  пјҺ
пјҺ 
-
пјҲ1пјү жұӮиҜҒпјҡ
 е№ійқў
е№ійқў пјӣ
пјӣ
-
пјҲ2пјү жұӮдәҢйқўи§’
 зҡ„жӯЈејҰеҖјпјҺ
зҡ„жӯЈејҰеҖјпјҺ
еңЁдёүжЈұй”Ҙ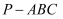 дёӯпјҢе№ійқў
дёӯпјҢе№ійқў е№ійқў
е№ійқў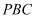 пјҢ
пјҢ 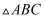 е’Ң
е’Ң йғҪжҳҜиҫ№й•ҝдёә
йғҪжҳҜиҫ№й•ҝдёә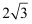 зҡ„зӯүиҫ№дёүи§’еҪўпјҢиӢҘ
зҡ„зӯүиҫ№дёүи§’еҪўпјҢиӢҘ дёәдёүжЈұй”Ҙ
дёәдёүжЈұй”Ҙ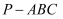 еӨ–жҺҘзҗғдёҠзҡ„еҠЁзӮ№пјҢеҲҷзӮ№
еӨ–жҺҘзҗғдёҠзҡ„еҠЁзӮ№пјҢеҲҷзӮ№ еҲ°е№ійқў
еҲ°е№ійқў и·қзҰ»зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
и·қзҰ»зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
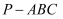 дёӯпјҢе№ійқў
дёӯпјҢе№ійқў е№ійқў
е№ійқў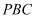 пјҢ
пјҢ 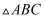 е’Ң
е’Ң йғҪжҳҜиҫ№й•ҝдёә
йғҪжҳҜиҫ№й•ҝдёә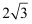 зҡ„зӯүиҫ№дёүи§’еҪўпјҢиӢҘ
зҡ„зӯүиҫ№дёүи§’еҪўпјҢиӢҘ дёәдёүжЈұй”Ҙ
дёәдёүжЈұй”Ҙ еӨ–жҺҘзҗғдёҠзҡ„еҠЁзӮ№пјҢеҲҷзӮ№
еӨ–жҺҘзҗғдёҠзҡ„еҠЁзӮ№пјҢеҲҷзӮ№ еҲ°е№ійқў
еҲ°е№ійқў и·қзҰ»зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
и·қзҰ»зҡ„жңҖеӨ§еҖјдёәпјҲ пјү
A .  B .
B .  C .
C . 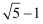 D .
D . 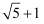
 B .
B .  C .
C . 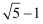 D .
D . 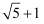
еңЁжЈұй•ҝдёә1зҡ„жӯЈж–№дҪ“ дёӯпјҢзӮ№
дёӯпјҢзӮ№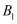 еҲ°е№ійқў
еҲ°е№ійқў зҡ„и·қзҰ»дёәпјҺ
зҡ„и·қзҰ»дёәпјҺ
 дёӯпјҢзӮ№
дёӯпјҢзӮ№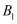 еҲ°е№ійқў
еҲ°е№ійқў зҡ„и·қзҰ»дёәпјҺ
зҡ„и·қзҰ»дёәпјҺ
еҰӮеӣҫпјҢеңЁеӣӣжЈұй”Ҙ  дёӯпјҢеә•йқўABCDжҳҜзҹ©еҪўпјҢе№ійқў
дёӯпјҢеә•йқўABCDжҳҜзҹ©еҪўпјҢе№ійқў  е№ійқўSBCпјҢ
е№ійқўSBCпјҢ  пјҢMжҳҜBCзҡ„дёӯзӮ№пјҢ
пјҢMжҳҜBCзҡ„дёӯзӮ№пјҢ 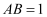 пјҢ
пјҢ 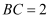 пјҺ
пјҺ
 дёӯпјҢеә•йқўABCDжҳҜзҹ©еҪўпјҢе№ійқў
дёӯпјҢеә•йқўABCDжҳҜзҹ©еҪўпјҢе№ійқў  е№ійқўSBCпјҢ
е№ійқўSBCпјҢ  пјҢMжҳҜBCзҡ„дёӯзӮ№пјҢ
пјҢMжҳҜBCзҡ„дёӯзӮ№пјҢ 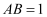 пјҢ
пјҢ 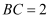 пјҺ
пјҺ 
-
пјҲ1пјү жұӮиҜҒпјҡ
 пјҺ
пјҺ
-
пјҲ2пјү иӢҘдәҢйқўи§’
 зҡ„жӯЈејҰеҖјдёә
зҡ„жӯЈејҰеҖјдёә  пјҢжұӮеӣӣжЈұй”Ҙ
пјҢжұӮеӣӣжЈұй”Ҙ  зҡ„дҪ“з§ҜпјҺ
зҡ„дҪ“з§ҜпјҺ
еҰӮеӣҫпјҢе№іиЎҢе…ӯйқўдҪ“ зҡ„еә•йқў
зҡ„еә•йқў жҳҜзҹ©еҪўпјҢPдёәжЈұ
жҳҜзҹ©еҪўпјҢPдёәжЈұ дёҠдёҖзӮ№.дё”
дёҠдёҖзӮ№.дё” пјҢ Fдёә
пјҢ Fдёә зҡ„дёӯзӮ№.
зҡ„дёӯзӮ№.
 зҡ„еә•йқў
зҡ„еә•йқў жҳҜзҹ©еҪўпјҢPдёәжЈұ
жҳҜзҹ©еҪўпјҢPдёәжЈұ дёҠдёҖзӮ№.дё”
дёҠдёҖзӮ№.дё” пјҢ Fдёә
пјҢ Fдёә зҡ„дёӯзӮ№.
зҡ„дёӯзӮ№.
-
пјҲ1пјү иҜҒжҳҺпјҡ
 пјӣ
пјӣ
-
пјҲ2пјү иӢҘ
 .еҪ“зӣҙзәҝPBдёҺе№ійқў
.еҪ“зӣҙзәҝPBдёҺе№ійқў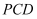 жүҖжҲҗзҡ„и§’дёә
жүҖжҲҗзҡ„и§’дёә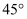 пјҢ дё”дәҢйқўи§’
пјҢ дё”дәҢйқўи§’ зҡ„е№ійқўи§’дёәй”җи§’ж—¶.жұӮдёүжЈұй”Ҙ
зҡ„е№ійқўи§’дёәй”җи§’ж—¶.жұӮдёүжЈұй”Ҙ зҡ„дҪ“з§Ҝ.
зҡ„дҪ“з§Ҝ.
еҰӮеӣҫпјҢеңЁзӣҙдёүжЈұжҹұ дёӯпјҢ
дёӯпјҢ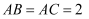 пјҢ
пјҢ  пјҢ
пјҢ 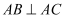 пјҢ
пјҢ  дәӨ
дәӨ дәҺзӮ№
дәҺзӮ№ пјҢ
пјҢ  дёә
дёә зҡ„дёӯзӮ№.
зҡ„дёӯзӮ№.
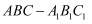 дёӯпјҢ
дёӯпјҢ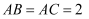 пјҢ
пјҢ  пјҢ
пјҢ 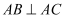 пјҢ
пјҢ  дәӨ
дәӨ дәҺзӮ№
дәҺзӮ№ пјҢ
пјҢ  дёә
дёә зҡ„дёӯзӮ№.
зҡ„дёӯзӮ№.
пјҲв… пјүжұӮиҜҒпјҡ е№ійқў
е№ійқў пјӣ
пјӣ
пјҲв…ЎпјүжұӮдәҢйқўи§’ зҡ„дҪҷејҰеҖј.
зҡ„дҪҷејҰеҖј.
еҰӮеӣҫ1пјҢеңЁ дёӯпјҢMAжҳҜBCиҫ№дёҠзҡ„й«ҳпјҢ
дёӯпјҢMAжҳҜBCиҫ№дёҠзҡ„й«ҳпјҢ пјҢ
пјҢ 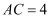 .еҰӮеӣҫ2пјҢе°Ҷ
.еҰӮеӣҫ2пјҢе°Ҷ жІҝMAиҝӣиЎҢзҝ»жҠҳпјҢдҪҝеҫ—дәҢйқўи§’
жІҝMAиҝӣиЎҢзҝ»жҠҳпјҢдҪҝеҫ—дәҢйқўи§’ дёә
дёә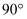 пјҢ еҶҚиҝҮзӮ№BдҪң
пјҢ еҶҚиҝҮзӮ№BдҪң пјҢ иҝһжҺҘADпјҢCDпјҢMDпјҢдё”
пјҢ иҝһжҺҘADпјҢCDпјҢMDпјҢдё” пјҢ
пјҢ  .
.
 дёӯпјҢMAжҳҜBCиҫ№дёҠзҡ„й«ҳпјҢ
дёӯпјҢMAжҳҜBCиҫ№дёҠзҡ„й«ҳпјҢ пјҢ
пјҢ 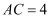 .еҰӮеӣҫ2пјҢе°Ҷ
.еҰӮеӣҫ2пјҢе°Ҷ жІҝMAиҝӣиЎҢзҝ»жҠҳпјҢдҪҝеҫ—дәҢйқўи§’
жІҝMAиҝӣиЎҢзҝ»жҠҳпјҢдҪҝеҫ—дәҢйқўи§’ дёә
дёә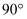 пјҢ еҶҚиҝҮзӮ№BдҪң
пјҢ еҶҚиҝҮзӮ№BдҪң пјҢ иҝһжҺҘADпјҢCDпјҢMDпјҢдё”
пјҢ иҝһжҺҘADпјҢCDпјҢMDпјҢдё” пјҢ
пјҢ  .
.
-
пјҲ1пјү жұӮиҜҒпјҡ
 е№ійқўMADпјӣ
е№ійқўMADпјӣ
-
пјҲ2пјү еңЁзәҝж®өMDдёҠеҸ–дёҖзӮ№EдҪҝ
 пјҢ жұӮзӣҙзәҝAEдёҺе№ійқўMBDжүҖжҲҗи§’зҡ„жӯЈејҰеҖј.
пјҢ жұӮзӣҙзәҝAEдёҺе№ійқўMBDжүҖжҲҗи§’зҡ„жӯЈејҰеҖј.
жңҖиҝ‘жӣҙж–°



