3.1 椭圆 知识点题库
以正方形的相对顶点A,C为焦点的椭圆恰好过正方形四边中点,则椭圆的离心率为 ( )
A .  B .
B .  C .
C . 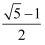 D .
D . 
 B .
B .  C .
C . 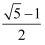 D .
D . 
如图,面ABC⊥α,D为AB的中点,|AB|=2,∠CDB=60°,P为α内的动点,且P到直线CD的距离为  ,则∠APB的最大值为( )
,则∠APB的最大值为( )
 ,则∠APB的最大值为( )
,则∠APB的最大值为( ) 
A . 30°
B . 60°
C . 90°
D . 120°
如图,椭圆E:  =1(a>b>0)经过点A(0,﹣1),且离心率为
=1(a>b>0)经过点A(0,﹣1),且离心率为 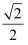 .
.
 =1(a>b>0)经过点A(0,﹣1),且离心率为
=1(a>b>0)经过点A(0,﹣1),且离心率为 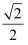 .
. (I)求椭圆E的方程;
(II)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),问直线AP与AQ的斜率之和是否为定值,若是,求出这个定值;若不是,请说明理由.

若椭圆  +
+  =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1, 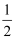 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是.
 +
+  =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1, 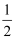 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是.
已知F1 , F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1= 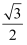 ,∠F1PF2=
,∠F1PF2= 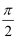 ,则双曲线C2的离心率e2的值为( )
,则双曲线C2的离心率e2的值为( )
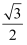 ,∠F1PF2=
,∠F1PF2= 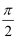 ,则双曲线C2的离心率e2的值为( )
,则双曲线C2的离心率e2的值为( )
A . 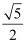 B .
B . 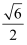 C .
C .  D .
D . 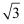
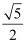 B .
B . 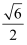 C .
C .  D .
D . 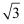
设椭圆的对称轴为坐标轴,短轴的一个端点与两焦点是同一个正三角形的顶点,焦点与椭圆上的点的最短距离为  ,则这个椭圆的方程为,离心率为.
,则这个椭圆的方程为,离心率为.
 ,则这个椭圆的方程为,离心率为.
,则这个椭圆的方程为,离心率为.
经过椭圆  的一个焦点作倾斜角为45°的直线
的一个焦点作倾斜角为45°的直线  ,交椭圆于
,交椭圆于 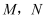 两点,设
两点,设  为坐标原点,则
为坐标原点,则  等于( )
等于( )
 的一个焦点作倾斜角为45°的直线
的一个焦点作倾斜角为45°的直线  ,交椭圆于
,交椭圆于 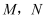 两点,设
两点,设  为坐标原点,则
为坐标原点,则  等于( )
等于( )
A . 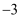 B .
B .  C .
C . 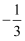 D .
D . 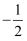
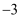 B .
B .  C .
C . 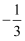 D .
D . 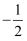
波罗尼斯(古希腊数学家,的公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,且k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有椭圆  =1(a>b>0),A,B为椭圆的长轴端点,C,D为椭圆的短轴端点,动点M满足
=1(a>b>0),A,B为椭圆的长轴端点,C,D为椭圆的短轴端点,动点M满足  =2,△MAB面积的最大值为8,△MCD面积的最小值为1,则椭圆的离心率为( )
=2,△MAB面积的最大值为8,△MCD面积的最小值为1,则椭圆的离心率为( )
 =1(a>b>0),A,B为椭圆的长轴端点,C,D为椭圆的短轴端点,动点M满足
=1(a>b>0),A,B为椭圆的长轴端点,C,D为椭圆的短轴端点,动点M满足  =2,△MAB面积的最大值为8,△MCD面积的最小值为1,则椭圆的离心率为( )
=2,△MAB面积的最大值为8,△MCD面积的最小值为1,则椭圆的离心率为( )
A .  B .
B . 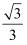 C .
C . 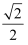 D .
D . 
 B .
B . 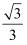 C .
C . 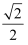 D .
D . 
已知椭圆  (
( 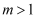 )与双曲线
)与双曲线  (
( 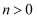 )的焦点重合,若双曲线的顶点是椭圆长轴的两个三等分点,曲线
)的焦点重合,若双曲线的顶点是椭圆长轴的两个三等分点,曲线 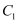 ,
,  的离心率分别为
的离心率分别为 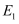 ,
, 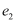 ,则
,则  的值为( )
的值为( )
 (
( 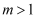 )与双曲线
)与双曲线  (
( 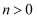 )的焦点重合,若双曲线的顶点是椭圆长轴的两个三等分点,曲线
)的焦点重合,若双曲线的顶点是椭圆长轴的两个三等分点,曲线 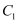 ,
,  的离心率分别为
的离心率分别为 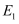 ,
, 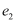 ,则
,则  的值为( )
的值为( )
A .  B .
B . 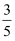 C .
C .  D .
D . 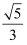
 B .
B . 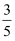 C .
C .  D .
D . 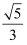
已知椭圆  的左右焦点分别为
的左右焦点分别为 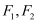 ,若以
,若以  为圆心,
为圆心, 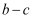 为半径作圆
为半径作圆  ,过椭圆上一点P作此圆的切线,切点为T,且
,过椭圆上一点P作此圆的切线,切点为T,且  的最小值不小于
的最小值不小于  ,则椭圆的离心率e的取值范围是( )
,则椭圆的离心率e的取值范围是( )
 的左右焦点分别为
的左右焦点分别为 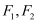 ,若以
,若以  为圆心,
为圆心, 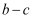 为半径作圆
为半径作圆  ,过椭圆上一点P作此圆的切线,切点为T,且
,过椭圆上一点P作此圆的切线,切点为T,且  的最小值不小于
的最小值不小于  ,则椭圆的离心率e的取值范围是( )
,则椭圆的离心率e的取值范围是( )
A .  B .
B .  C .
C . 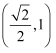 D .
D . 
 B .
B .  C .
C . 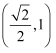 D .
D . 
若椭圆的焦距长等于它的短轴长,则椭圆的离心率等于( )
A .  B .
B .  C .
C . 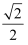 D . 2
D . 2
 B .
B .  C .
C . 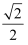 D . 2
D . 2
如果椭圆  +
+  =1上一点P到焦点F1的距离等于10,那么点P到另一个焦点F2的距离是.
=1上一点P到焦点F1的距离等于10,那么点P到另一个焦点F2的距离是.
 +
+  =1上一点P到焦点F1的距离等于10,那么点P到另一个焦点F2的距离是.
=1上一点P到焦点F1的距离等于10,那么点P到另一个焦点F2的距离是.
椭圆  的左右焦点分别是
的左右焦点分别是 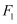 、
、  ,以
,以  为圆心的圆过椭圆的中心,且与椭圆交于点P,若直线
为圆心的圆过椭圆的中心,且与椭圆交于点P,若直线 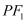 恰好与圆
恰好与圆  相切于点P,则椭圆的离心率为( )
相切于点P,则椭圆的离心率为( )
 的左右焦点分别是
的左右焦点分别是 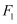 、
、  ,以
,以  为圆心的圆过椭圆的中心,且与椭圆交于点P,若直线
为圆心的圆过椭圆的中心,且与椭圆交于点P,若直线 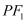 恰好与圆
恰好与圆  相切于点P,则椭圆的离心率为( )
相切于点P,则椭圆的离心率为( )
A . 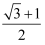 B .
B . 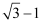 C .
C . 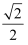 D .
D . 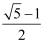
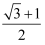 B .
B . 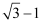 C .
C . 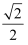 D .
D . 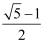
已知椭圆  的长轴长为
的长轴长为 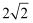 ,离心率
,离心率  ,过右焦点
,过右焦点  的直线
的直线  交椭圆于
交椭圆于  、
、 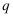 两点.
两点.
 的长轴长为
的长轴长为 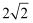 ,离心率
,离心率  ,过右焦点
,过右焦点  的直线
的直线  交椭圆于
交椭圆于  、
、 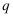 两点.
两点.
-
(1) 求椭圆的方程.
-
(2) 当直线
 的斜率为
的斜率为  时,求
时,求 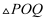 的面积.
的面积.
已知椭圆  右焦点为F
右焦点为F 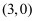 过点F的直线交E于A,B两点,若AB的中点坐标为
过点F的直线交E于A,B两点,若AB的中点坐标为  ,则E的离心率是( )
,则E的离心率是( )
 右焦点为F
右焦点为F 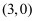 过点F的直线交E于A,B两点,若AB的中点坐标为
过点F的直线交E于A,B两点,若AB的中点坐标为  ,则E的离心率是( )
,则E的离心率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
过椭圆  的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为.
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为.
 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为.
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为.
已知椭圆  的左、右焦点分别为
的左、右焦点分别为 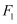 、
、  ,过
,过 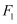 的直线与椭圆交于
的直线与椭圆交于  、
、  两点,若
两点,若  的周长为
的周长为 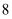 ,则
,则 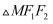 面积的最大值为( )
面积的最大值为( )
 的左、右焦点分别为
的左、右焦点分别为 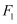 、
、  ,过
,过 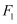 的直线与椭圆交于
的直线与椭圆交于  、
、  两点,若
两点,若  的周长为
的周长为 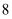 ,则
,则 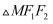 面积的最大值为( )
面积的最大值为( )
A .  B .
B .  C .
C . 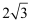 D . 3
D . 3
 B .
B .  C .
C . 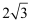 D . 3
D . 3
在平面直角坐标系  中,过椭圆
中,过椭圆 
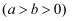
 中,过椭圆
中,过椭圆 
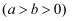
右焦点的直线  交
交  于
于  ,
,  两点,
两点,  为
为  的中点,且
的中点,且 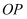 的斜率为
的斜率为  .
.
(Ⅰ)求椭圆  的方程;
的方程;
(Ⅱ)已知  ,
,  为
为  上的两点,若四边形
上的两点,若四边形  的对角线
的对角线 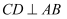 ,求四边形
,求四边形  面积的最大值.
面积的最大值.
已知动点M到定点F(1,0)的距离与到定直线 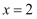 的距离之比为定值
的距离之比为定值 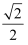 .
.
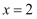 的距离之比为定值
的距离之比为定值 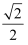 .
.
-
(1) 求动点M轨迹L的方程;
-
(2) 设L的左、右焦点分别为
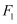 ,
,  ,过点
,过点  作直线l与轨迹L交于A,B两点,
作直线l与轨迹L交于A,B两点,  ,求
,求  的面积.
的面积.
已知椭圆 过点
过点 离心率
离心率 , 左、右焦点分别为
, 左、右焦点分别为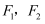 , P,Q是椭圆C上位于x轴上方的两点.
, P,Q是椭圆C上位于x轴上方的两点.
 过点
过点 离心率
离心率 , 左、右焦点分别为
, 左、右焦点分别为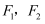 , P,Q是椭圆C上位于x轴上方的两点.
, P,Q是椭圆C上位于x轴上方的两点.
-
(1) 若
 , 求直线
, 求直线 的方程;
的方程;
-
(2) 延长
 分别交椭圆C于点M,N,设
分别交椭圆C于点M,N,设 , 求
, 求 的最小值.
的最小值.
最近更新



