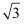旋转的性质 知识点题库

在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒  个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.

-
(1) 当点P移动到点D时,求出此时t的值;
-
(2) 当t为何值时,△PQB为直角三角形;
-
(3) 已知过O、P、Q三点的抛物线解析式为y=﹣
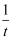 (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
 ,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为( )
 B . 4
C . 2
D . 1
B . 4
C . 2
D . 1
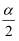 ,连接PB,试探究PA、PB、PC满足的等量关系.
,连接PB,试探究PA、PB、PC满足的等量关系.
-
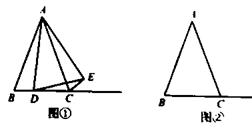
(1) 当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为;
-
(2) 如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
-
(3) PA、PB、PC满足的等量关系为.
下面的证法供你参考:
把△ACD绕点A顺时针旋转60°得到△ABE,连接ED,则有△ACD≌△ABE,DC=EB,∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,∴AD=DE.在△DBE中,BD+EB>DE,即:BD+DC>AD
实践探索:

-
(1) 请你仿照上面的思路,探索解决下面的问题:
如图3,点D是等腰直角三角形△ABC边上的点(点D不与B、C重合).求证:BD+DC>
 AD.
AD. -
(2) 如果点D运动到等腰直角三角形△ABC外或内时,BD、DC和AD之间又存在怎样的数量关系?直接写出结论.
-
(3) 已知:如图4,等腰△ABC中,AB=AC,且∠BAC=α(α为钝角),D是等腰△ABC外一点,且∠BDC+∠BAC=180°,BD、DC与AD之间存在怎样的数量关系?写出你的猜想,并证明.
 中,
中,  ,
,  绕点
绕点  顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交 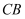 ,
,  (或它们的延长线)于点
(或它们的延长线)于点  ,
,  。当
。当  绕点
绕点  旋转到
旋转到 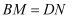 时(如图1),易证
时(如图1),易证  .(不必证明)
.(不必证明) 


-
(1) 当
 绕点
绕点  旋转到
旋转到  时(如图2),线段
时(如图2),线段 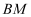 ,
, 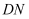 和
和 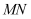 之间有怎样的数量关系?写出猜想,并加以证明。
之间有怎样的数量关系?写出猜想,并加以证明。
-
(2) 当
 绕点
绕点  旋转到如图3的位置时,线段
旋转到如图3的位置时,线段 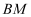 ,
, 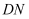 和
和 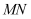 之间又有怎样的数量关系?写出猜想,并加以证明。
之间又有怎样的数量关系?写出猜想,并加以证明。
-
(1) 当点D在边BC上,求证:△BAD≌△CAE。
-
(2) 当点D在边BC上,若∠BAC=a,求∠DCE的大小.(用含a的代数式表示)。
-
(3) 当DE与△ABC的边所在的直线垂直,且∠BAC=40°时,请借助图②,直接写出∠CED的大小。

 B . 3
C .
B . 3
C .  D . 1+
D . 1+ 
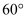 角的三角板放置在一条直线上,
角的三角板放置在一条直线上,  边与直线
边与直线 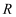 重合,
重合,  边的垂直平分线与边
边的垂直平分线与边 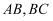 分别交于
分别交于  两点,连接
两点,连接 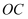 .
.
-
(1)
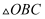 是三角形;
是三角形;
-
(2) 直线
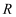 上有一动点
上有一动点  (不与点
(不与点 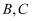 重合) ,连接
重合) ,连接 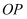 并把
并把 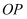 绕点
绕点  顺时针旋转
顺时针旋转 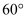 到
到 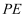 ,连接
,连接 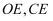 .当点
.当点  在图2所示的位置时,证明
在图2所示的位置时,证明  .我们可以用
.我们可以用  来证明
来证明  ,从而得到
,从而得到  .当点
.当点  移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
-
(3) 当点
 在
在  边上移动时(不与点
边上移动时(不与点 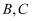 重合),
重合),  周长的最小值是.
周长的最小值是.

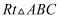 中,
中, 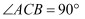 ,
, 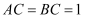 ,且
,且 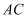 边在直线
边在直线  上,将
上,将 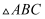 绕点
绕点  顺时针旋转到位置可得到点
顺时针旋转到位置可得到点  ,此时
,此时  ;将①位置的三角形绕点
;将①位置的三角形绕点  顺时针旋转到②位置,可得到点
顺时针旋转到②位置,可得到点 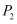 ,此时
,此时  ;将②位置的三角形绕点
;将②位置的三角形绕点 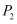 顺时针旋转到③位置,可得到点
顺时针旋转到③位置,可得到点  ,此时
,此时 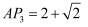 ;…,按此规律垂线旋转,直至得到点
;…,按此规律垂线旋转,直至得到点  为止,则
为止,则  ( ).
( ). 
 B .
B .  C .
C . 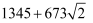 D .
D . 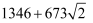

-
(1) 判断∠CAF与∠DAG是否相等,并说明理由.
-
(2) 求证:△ACF≌△ADG .

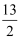 ,
,  )
B . (6,0)
C . (
)
B . (6,0)
C . ( 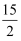 ,
,  )
D . (7,0)
)
D . (7,0)

-
(1) 当点D'恰好落在EF边上时,求旋转角a的值;
-
(2) 如图2,G为BC中点,且0°<a之90°,求证:GD'=E'D;
-
(3) 小长方形CEFD绕点C顺时针旋转一周的过程中,△ DCD'与A CBD'能否全等?若能,直接写出旋转角α的值:若不能说明理由.
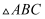 按顺时针方向转动40°得
按顺时针方向转动40°得 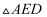 ,点D恰好在边BC上,则∠C=°.
,点D恰好在边BC上,则∠C=°. 
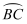 长度为 .(结果保留π)
长度为 .(结果保留π)


-
(1) (发现证明)
问题:如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且
 ,求证:
,求证:  .
.观察:EF、DF、BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?
思路:将
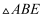 绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的
绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的 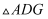 .
.①根据上述思路在图1中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?(写出详细的解答过程)
-
(2) (类比迁移)
若点E、F分别为正方形两条边的延长线上的动点,EF、BE、DF三者之间还存在(1)中的关系吗?根据解决(1)中问题的经验加以探究.
①如图2,在正方形ABCD中,点E、F分别是CB、DC延长线上的动点,且
 ,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.
,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.②如图3,在正方形ABCD中,点E、F分别是BC、CD延长线上的动点,且
 ,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).
,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).
 中,
中, 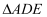 绕点
绕点  顺时针旋转
顺时针旋转 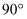 后与
后与  重合,
重合, 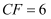 ,
, 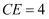 ,则
,则 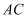 的长度为( )
的长度为( ) 
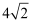 C . 5
D .
C . 5
D . 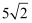
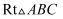 中,
中,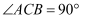 ,
, 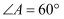 ,
,  , 将
, 将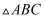 绕点C按逆时针方向旋转得到
绕点C按逆时针方向旋转得到 , 此时点
, 此时点 恰好在
恰好在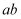 边上,则点
边上,则点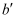 与点B之间的距离为( )
与点B之间的距离为( )
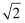 D .
D .