向量方法证明线、面的位置关系定理 知识点题库
如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.

如图,在棱长为1的正方体  中,点E是棱AB上的动点.
中,点E是棱AB上的动点.
 中,点E是棱AB上的动点.
中,点E是棱AB上的动点.
-
(1) 求证:
 ;
;
-
(2) 若直线
 与平面
与平面  所成的角是45
所成的角是45  ,请你确定点E的位置,并证明你的结论.
,请你确定点E的位置,并证明你的结论.
已知三棱柱  中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 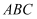 为等腰直角三角形,
为等腰直角三角形,  ,点
,点  为棱
为棱  的中点,点
的中点,点  在棱
在棱  上运动.
上运动.
 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面 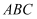 为等腰直角三角形,
为等腰直角三角形,  ,点
,点  为棱
为棱  的中点,点
的中点,点  在棱
在棱  上运动.
上运动. 
-
(1) 求证
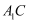
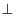
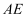 ;
;
-
(2) 当点
 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角  的平面角的余弦值为
的平面角的余弦值为 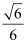 ,求点
,求点  到平面
到平面  的距离;
的距离;
-
(3) 在(2)的条件下,试确定线段
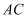 上是否存在一点
上是否存在一点  ,使得
,使得 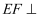 平面
平面  ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
如图,在四棱锥  中,侧棱
中,侧棱  底面
底面  ,底面
,底面  是直角梯形,
是直角梯形, 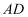 ∥
∥  ,
,  ,且
,且  ,
, 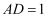 ,
,  是棱
是棱  的中点.
的中点.
 中,侧棱
中,侧棱  底面
底面  ,底面
,底面  是直角梯形,
是直角梯形, 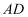 ∥
∥  ,
,  ,且
,且  ,
, 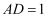 ,
,  是棱
是棱  的中点.
的中点. 
-
(1) 求证:
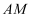 ∥平面
∥平面  ;
;
-
(2) 求平面
 与平面
与平面  所成锐二面角的余弦值;
所成锐二面角的余弦值;
-
(3) 设点
 是线段
是线段 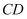 上的动点,
上的动点, 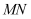 与平面
与平面  所成的角为
所成的角为 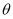 ,求
,求 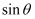 的最大值.
的最大值.
若点  为点
为点  在平面
在平面 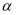 上的正投影,则记
上的正投影,则记  .如图,在棱长为
.如图,在棱长为  的正方体
的正方体  中,记平面
中,记平面  为
为 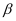 ,平面
,平面  为
为 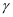 ,点
,点  是棱
是棱  上一动点(与
上一动点(与  、
、 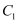 不重合)
不重合)  ,
,  .给出下列三个结论:
.给出下列三个结论:
 为点
为点  在平面
在平面 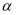 上的正投影,则记
上的正投影,则记  .如图,在棱长为
.如图,在棱长为  的正方体
的正方体  中,记平面
中,记平面  为
为 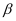 ,平面
,平面  为
为 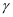 ,点
,点  是棱
是棱  上一动点(与
上一动点(与  、
、 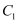 不重合)
不重合)  ,
,  .给出下列三个结论:
.给出下列三个结论: 
①线段  长度的取值范围是
长度的取值范围是  ;②存在点
;②存在点  使得
使得  平面
平面 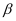 ;③存在点
;③存在点  使得
使得  .其中,所有正确结论的序号是( )
.其中,所有正确结论的序号是( )
A . ①②③
B . ②③
C . ①③
D . ①②
如图,在四棱柱  中,侧棱
中,侧棱  底面
底面  ,
, 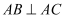 ,
, 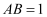 ,
,  ,
,  ,且点
,且点  和
和  分别为
分别为  和
和  的中点.
的中点.
 中,侧棱
中,侧棱  底面
底面  ,
, 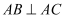 ,
, 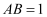 ,
,  ,
,  ,且点
,且点  和
和  分别为
分别为  和
和  的中点.
的中点. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 求二面角
 的正弦值;
的正弦值;
-
(3) 设
 为棱
为棱  上的点,若直线
上的点,若直线  和平面
和平面  所成角的正弦值为
所成角的正弦值为 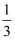 ,求线段
,求线段  的长.
的长.
如图,在四棱锥 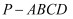 中,
中, 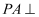 平面
平面  ,
,  ,
, 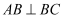 ,
,  ,
,  ,
,  为
为 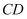 的中点,
的中点,  在
在  上,且
上,且  .
.
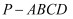 中,
中, 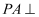 平面
平面  ,
,  ,
, 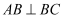 ,
,  ,
,  ,
,  为
为 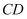 的中点,
的中点,  在
在  上,且
上,且  .
. 
-
(1) 求证:
 平面
平面 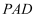 ;
;
-
(2) 求平面
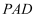 与平面
与平面 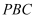 所成锐二面角的余弦值;
所成锐二面角的余弦值;
-
(3) 点
 是线段
是线段  上异于两端点的任意一点,若满足异面直线
上异于两端点的任意一点,若满足异面直线 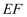 与
与 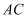 所成角为
所成角为 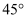 ,求
,求 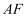 的长.
的长.
如图,在四棱锥 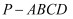 中,底面
中,底面  为直角梯形,
为直角梯形,  ,
,  且
且 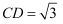 ,E为
,E为 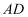 的中点,F是棱
的中点,F是棱 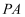 的中点,
的中点,  ,
,  底面
底面  .
. 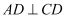
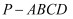 中,底面
中,底面  为直角梯形,
为直角梯形,  ,
,  且
且 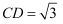 ,E为
,E为 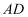 的中点,F是棱
的中点,F是棱 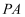 的中点,
的中点,  ,
,  底面
底面  .
. 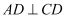

(Ⅰ)证明:  平面
平面  ;
;
(Ⅱ)求二面角  的正弦值;
的正弦值;
(Ⅲ)在线段 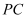 (不含端点)上是否存在一点M,使得直线
(不含端点)上是否存在一点M,使得直线 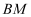 和平面
和平面 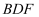 所成角的正弦值为
所成角的正弦值为  ?若存在,求出此时
?若存在,求出此时 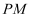 的长;若不存在,说明理由.
的长;若不存在,说明理由.
如图,在以  ,
,  ,
,  ,
,  ,
,  ,
,  为顶点的多面体中,四边形
为顶点的多面体中,四边形  是矩形,
是矩形, 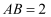 ,
,  ,
,  平面
平面  ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  ,
,  ,
,  为顶点的多面体中,四边形
为顶点的多面体中,四边形  是矩形,
是矩形, 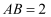 ,
,  ,
,  平面
平面  ,
,  ,
,  .
. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 求二面角
 的余弦值.
的余弦值.
如图所示,在四棱锥 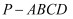 中,底面
中,底面  是矩形,
是矩形, 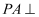 底面
底面  ,
,  ,
, 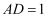 ,
,  是
是  的中点,作
的中点,作  交
交 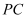 于点
于点  ,且
,且  .
.
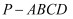 中,底面
中,底面  是矩形,
是矩形, 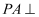 底面
底面  ,
,  ,
, 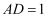 ,
,  是
是  的中点,作
的中点,作  交
交 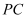 于点
于点  ,且
,且  .
. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 求平面
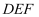 与平面
与平面  的夹角的余弦值.
的夹角的余弦值.
如图,在三棱柱ABC﹣A1B1C1中,四边形ACC1A1和BCC1B1均为正方形,且所在平面互相垂直.
(Ⅰ)求证:BC1⊥AB1;
(Ⅱ)求直线BC1与平面AB1C1所成角的大小.

如图,在多面体  中,
中,  平面
平面  ,
,  是平行四边形,且
是平行四边形,且 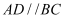 ,
,  ,
,  ,
, 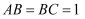 .
.
 中,
中,  平面
平面  ,
,  是平行四边形,且
是平行四边形,且 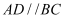 ,
,  ,
,  ,
, 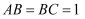 .
. 
-
(1) 求证:
 ;
;
-
(2) 求二面角
 的余弦值;
的余弦值;
-
(3) 若点
 在棱
在棱 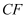 上,直线
上,直线  与平面
与平面 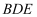 所成角的正弦值为
所成角的正弦值为 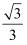 ,求线段
,求线段 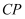 的长.
的长.
如图,在三棱柱 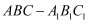 中,
中,  平面
平面  ,且
,且 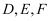 分别为棱
分别为棱  的中点.
的中点.
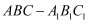 中,
中,  平面
平面  ,且
,且 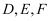 分别为棱
分别为棱  的中点.
的中点. 
-
(1) 证明:直线
 与
与 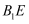 共面,并求其所成角的余弦值;
共面,并求其所成角的余弦值;
-
(2) 在棱
 上是否存在点M,使得
上是否存在点M,使得  平面
平面  ,若存在,求
,若存在,求  的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM,

-
(1) 求BC;
-
(2) 求二面角A-PM-B的正弦值。
如图,在多面体 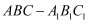 中,侧面
中,侧面  为菱形,
为菱形,  平面
平面 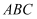 ,
,  平面
平面 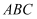 ,
,  ,
,  是
是 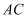 的中点,
的中点,  为棱
为棱  上的动点,
上的动点,  .
.
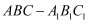 中,侧面
中,侧面  为菱形,
为菱形,  平面
平面 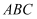 ,
,  平面
平面 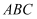 ,
,  ,
,  是
是 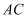 的中点,
的中点,  为棱
为棱  上的动点,
上的动点,  .
. 
-
(1) 证明:平面
 平面
平面  ;
;
-
(2) 当点
 位于棱
位于棱  的什么位置时,面
的什么位置时,面  与面
与面  ,所成的二面角的正弦值最小?
,所成的二面角的正弦值最小?
如图,正方体  的棱长为2,点E,F分别在棱BC,CD上运动,且
的棱长为2,点E,F分别在棱BC,CD上运动,且 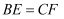 .
.
 的棱长为2,点E,F分别在棱BC,CD上运动,且
的棱长为2,点E,F分别在棱BC,CD上运动,且 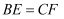 .
. 
-
(1) 求证:
 ;
;
-
(2) 求三棱锥
 的体积的最大值:
的体积的最大值:
-
(3) 当E,F分别是棱BC,CD的中点时,求平面
 与平面
与平面  的夹角的正弦值.
的夹角的正弦值.
如图,在正四棱锥 中,
中, ,
,  , P在侧棱
, P在侧棱 上,
上, 平面
平面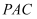 .
.
 中,
中, ,
,  , P在侧棱
, P在侧棱 上,
上, 平面
平面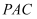 .
.
-
(1) 求平面
 与平面
与平面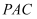 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
-
(2) 侧棱
 上是否存在一点E,使得
上是否存在一点E,使得 平面
平面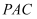 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在四棱锥P – ABCD中,PA⊥平面ABCD,AD ⊥ CD,AD // BC,PA = AD = CD = 2,BC = 3.E为PD的中点,点F在PC上,且 .
.
 .
. 
-
(1) 求证:CD⊥平面PAD;
-
(2) 求二面角F – AE – P的余弦值;
-
(3) 设点G在PB上,且
 . 判断直线AG是否在平面AEF内,说明理由.
. 判断直线AG是否在平面AEF内,说明理由.
如图(1),已知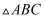 是边长为6的等边三角形,点
是边长为6的等边三角形,点 ,
,  分别在
分别在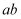 ,
, 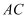 上,
上, ,
,  是线段
是线段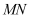 的中点.将
的中点.将 沿直线
沿直线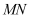 进行翻折,
进行翻折, 翻折到点
翻折到点 , 使得二面角
, 使得二面角 是直二面角,如图(2).
是直二面角,如图(2).
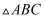 是边长为6的等边三角形,点
是边长为6的等边三角形,点 ,
,  分别在
分别在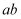 ,
, 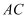 上,
上, ,
,  是线段
是线段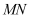 的中点.将
的中点.将 沿直线
沿直线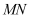 进行翻折,
进行翻折, 翻折到点
翻折到点 , 使得二面角
, 使得二面角 是直二面角,如图(2).
是直二面角,如图(2).
-
(1) 若
 平面
平面 , 求
, 求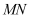 的长;
的长;
-
(2) 求二面角
 的余弦值.
的余弦值.
如图,在四棱锥 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,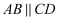 ,
, 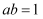 ,
,  ,
,  ,
,  , 平面
, 平面 平面ABCD,且
平面ABCD,且 , E为BC的中点.
, E为BC的中点.
 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,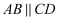 ,
, 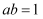 ,
,  ,
,  ,
,  , 平面
, 平面 平面ABCD,且
平面ABCD,且 , E为BC的中点.
, E为BC的中点.
-
(1) 证明:平面
 平面PBD.
平面PBD.
-
(2) 若四棱锥
 的体积为
的体积为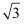 , 求二面角
, 求二面角 的余弦值.
的余弦值.
最近更新



