两点间的距离公式 知识点题库
在极坐标系中,已知两点A(2,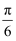 ),B(2,﹣
),B(2,﹣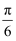 ),则|AB|=( )
),则|AB|=( )
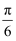 ),B(2,﹣
),B(2,﹣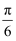 ),则|AB|=( )
),则|AB|=( )
A .  B . 2
C . 2
B . 2
C . 2 D . 4
D . 4
 B . 2
C . 2
B . 2
C . 2 D . 4
D . 4
在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,求点P的坐标.
已知点A(2,1),B(﹣2,3),C(0,1),则△ABC中,BC边上的中线长为.
已知 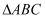 三边所在直线方程:
三边所在直线方程:  ,
,  ,
,  (
(  ).
).
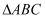 三边所在直线方程:
三边所在直线方程:  ,
,  ,
,  (
(  ).
).
-
(1) 判断
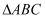 的形状;
的形状;
-
(2) 当
 边上的高为1时,求
边上的高为1时,求  的值.
的值.
已知直角三角形ABC中,直角边AC=6,点D是边AC上一定点,CD=2,点P是斜边AB上一动点,,CP⊥BD,则△  面积的最大值是;线段
面积的最大值是;线段 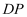 长度的最小值是.
长度的最小值是.
 面积的最大值是;线段
面积的最大值是;线段 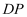 长度的最小值是.
长度的最小值是.
在平面直角坐标系  中,抛物线
中,抛物线  上的点
上的点  到其焦点的距离为3,则点
到其焦点的距离为3,则点  到点
到点  的距离为.
的距离为.
 中,抛物线
中,抛物线  上的点
上的点  到其焦点的距离为3,则点
到其焦点的距离为3,则点  到点
到点  的距离为.
的距离为.
在直角坐标系x0y中,把曲线 
 α为参数)上每个点的横坐标变为原来的
α为参数)上每个点的横坐标变为原来的  倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线  以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线
以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线 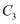 的极坐标方程
的极坐标方程 

 α为参数)上每个点的横坐标变为原来的
α为参数)上每个点的横坐标变为原来的  倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线  以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线
以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线 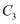 的极坐标方程
的极坐标方程 
-
(1) 写出
 的普通方程和
的普通方程和 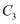 的直角坐标方程;
的直角坐标方程;
-
(2) 设点M在
 上,点N在
上,点N在 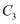 上,求|MN|的最小值以及此时M的直角坐标.
上,求|MN|的最小值以及此时M的直角坐标.
已知圆  和两点
和两点  ,若圆
,若圆  上存在点
上存在点  ,使得
,使得 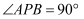 ,则
,则  的最大值为( )
的最大值为( )
 和两点
和两点  ,若圆
,若圆  上存在点
上存在点  ,使得
,使得 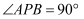 ,则
,则  的最大值为( )
的最大值为( )
A . 8
B . 9
C . 10
D . 11
在平面直角坐标系  中,以原点
中,以原点  为极点,
为极点,  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 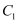 的参数方程为
的参数方程为  (
( 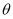 为参数),曲线
为参数),曲线  的极坐标方程为
的极坐标方程为  .
.
 中,以原点
中,以原点  为极点,
为极点,  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线 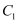 的参数方程为
的参数方程为  (
( 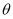 为参数),曲线
为参数),曲线  的极坐标方程为
的极坐标方程为  .
.
-
(1) 求曲线
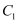 的普通方程和曲线
的普通方程和曲线  的直角坐标方程;
的直角坐标方程;
-
(2) 设
 为曲线
为曲线 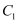 上一点,
上一点, 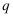 为曲线
为曲线  上一点,求
上一点,求 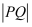 的最小值.
的最小值.
过点P(3,1)作⊙  的两条切线,切点分别为A、B,则弦AB的长为.
的两条切线,切点分别为A、B,则弦AB的长为.
 的两条切线,切点分别为A、B,则弦AB的长为.
的两条切线,切点分别为A、B,则弦AB的长为.
若实数 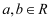 且
且 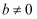 ,则
,则  的最小值为.
的最小值为.
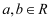 且
且 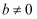 ,则
,则  的最小值为.
的最小值为.
设抛物线  的焦点为
的焦点为  ,直线
,直线  与
与  交于
交于 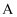 ,
,  ,与
,与 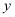 轴交于
轴交于 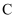 ,若
,若  ,则
,则  .
.
 的焦点为
的焦点为  ,直线
,直线  与
与  交于
交于 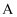 ,
,  ,与
,与 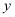 轴交于
轴交于 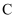 ,若
,若  ,则
,则  .
.
已知抛物线  的焦点为
的焦点为  ,准线为
,准线为  ,点
,点  是
是  上一点,过点
上一点,过点  作
作 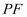 的垂线交
的垂线交  轴的正半轴于点
轴的正半轴于点  ,
, 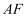 交抛物线于点
交抛物线于点  ,
,  与
与 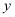 轴平行,则
轴平行,则  .
.
 的焦点为
的焦点为  ,准线为
,准线为  ,点
,点  是
是  上一点,过点
上一点,过点  作
作 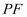 的垂线交
的垂线交  轴的正半轴于点
轴的正半轴于点  ,
, 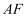 交抛物线于点
交抛物线于点  ,
,  与
与 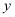 轴平行,则
轴平行,则  .
.
在平面直角坐标系  中,以坐标原点为极点,
中,以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线  的参数方程为:
的参数方程为:  (
( 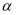 为参数),直线
为参数),直线  的极坐标方程为:
的极坐标方程为:  .
.
 中,以坐标原点为极点,
中,以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线  的参数方程为:
的参数方程为:  (
( 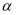 为参数),直线
为参数),直线  的极坐标方程为:
的极坐标方程为:  .
.
-
(1) 求曲线
 的普通方程和直线
的普通方程和直线  的直角坐标方程;
的直角坐标方程;
-
(2) 设
 ,
,  是曲线
是曲线  与直线
与直线  的公共点,
的公共点,  ,求
,求  的值.
的值.
到点 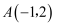 的距离为1的点
的距离为1的点 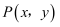 所满足的条件是.
所满足的条件是.
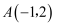 的距离为1的点
的距离为1的点 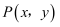 所满足的条件是.
所满足的条件是.
18世纪末期,挪威测量学家威塞尔首次利用坐标平面上的点来表示复数,使复数及其运算具有了几何意义,例如, 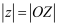 ,也即复数
,也即复数 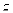 的模的几何意义为
的模的几何意义为 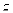 对应的点
对应的点 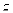 到原点的距离.在复平面内,复数
到原点的距离.在复平面内,复数 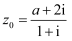 (
( 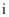 是虚数单位,
是虚数单位,  )是纯虚数,其对应的点为
)是纯虚数,其对应的点为  ,满足条件
,满足条件 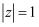 的点
的点 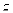 与
与  之间的最大距离为( )
之间的最大距离为( )
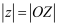 ,也即复数
,也即复数 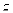 的模的几何意义为
的模的几何意义为 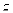 对应的点
对应的点 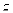 到原点的距离.在复平面内,复数
到原点的距离.在复平面内,复数 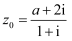 (
( 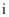 是虚数单位,
是虚数单位,  )是纯虚数,其对应的点为
)是纯虚数,其对应的点为  ,满足条件
,满足条件 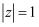 的点
的点 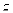 与
与  之间的最大距离为( )
之间的最大距离为( )
A . 1
B . 2
C . 3
D . 4
设复数  i,
i,  i,记复数
i,记复数 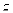 与
与  分别对应复平面内的点
分别对应复平面内的点  和
和  .
.
 i,
i,  i,记复数
i,记复数 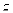 与
与  分别对应复平面内的点
分别对应复平面内的点  和
和  .
.
-
(1) 根据复数及其运算的几何意义,求
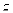 和
和  两点间的距离;
两点间的距离;
-
(2) 已知
 (
( 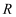 为正实数)表示动点
为正实数)表示动点 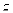 的集合是以点
的集合是以点  为圆心,
为圆心, 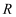 为半径的圆.那么满足条件
为半径的圆.那么满足条件  的点
的点 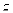 的集合是什么图形?并求出该图形的面积.
的集合是什么图形?并求出该图形的面积.
已知点 ,
,  ,
,  .求:
.求:
 ,
,  ,
,  .求:
.求:
-
(1) BC边上的中线所在直线的方程;
-
(2) 三角形ABC的面积.
在极坐标系中,已知直线 和曲线
和曲线 , 以极点为坐标原点,极轴为
, 以极点为坐标原点,极轴为 轴的正半轴建立直角坐标系.
轴的正半轴建立直角坐标系.
 和曲线
和曲线 , 以极点为坐标原点,极轴为
, 以极点为坐标原点,极轴为 轴的正半轴建立直角坐标系.
轴的正半轴建立直角坐标系.
-
(1) 求
 与
与 的直角坐标方程;
的直角坐标方程;
-
(2) 若
 与
与 交于A,B两点,且点
交于A,B两点,且点 , 求
, 求 的值.
的值.
“曼哈顿距离”也叫“出租车距离”,是19世纪德国犹太人数学家赫尔曼·闵可夫斯基首先提出来的名词,用来表示两个点在标准坐标系上的绝对轴距总和,即在直角坐标平面内,若 ,
,  , 则
, 则 ,
,  两点的“曼哈顿距离”为
两点的“曼哈顿距离”为 , 下列直角梯形中的虚线可以作为
, 下列直角梯形中的虚线可以作为 ,
,  两点的“曼哈顿距离”是( )
两点的“曼哈顿距离”是( )
 ,
,  , 则
, 则 ,
,  两点的“曼哈顿距离”为
两点的“曼哈顿距离”为 , 下列直角梯形中的虚线可以作为
, 下列直角梯形中的虚线可以作为 ,
,  两点的“曼哈顿距离”是( )
两点的“曼哈顿距离”是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
最近更新



