双曲线的应用 知识点题库
从双曲线 的左焦点F引圆
的左焦点F引圆 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则  与b-a的大小关系为 ( )
与b-a的大小关系为 ( )
A .  B .
B .  C .
C .  D . 不能确定
D . 不能确定
 B .
B .  C .
C .  D . 不能确定
D . 不能确定
过双曲线 的右焦点F,作渐近线
的右焦点F,作渐近线 的垂线与双曲线左右两支都相交,则双曲线的离心率e的取值范围为 ( )
的垂线与双曲线左右两支都相交,则双曲线的离心率e的取值范围为 ( )
 的右焦点F,作渐近线
的右焦点F,作渐近线 的垂线与双曲线左右两支都相交,则双曲线的离心率e的取值范围为 ( )
的垂线与双曲线左右两支都相交,则双曲线的离心率e的取值范围为 ( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设双曲线 的左,右焦点分别为
的左,右焦点分别为 , 过
, 过 的直线l交双曲线左支于A,B两点,则
的直线l交双曲线左支于A,B两点,则 的最小值为( )
的最小值为( )
 的左,右焦点分别为
的左,右焦点分别为 , 过
, 过 的直线l交双曲线左支于A,B两点,则
的直线l交双曲线左支于A,B两点,则 的最小值为( )
的最小值为( )
A . 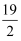 B . 11
C . 12
D . 16
B . 11
C . 12
D . 16
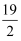 B . 11
C . 12
D . 16
B . 11
C . 12
D . 16
设F1和F2是双曲线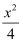 ﹣y2=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是
﹣y2=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是
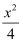 ﹣y2=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是
﹣y2=1的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是
过双曲线的一个焦点F2作垂直于实轴的直线,交双曲线于P、Q,F1是另一焦点,若∠PF1Q= 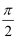 ,则双曲线的离心率e等于( )
,则双曲线的离心率e等于( )
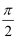 ,则双曲线的离心率e等于( )
,则双曲线的离心率e等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知双曲线C:  ﹣
﹣  =1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
 ﹣
﹣  =1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
A .  B .
B . 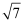 C .
C .  D .
D . 
 B .
B . 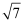 C .
C .  D .
D . 
过双曲线  的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
 的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知双曲线M:  =1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e=
=1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e= 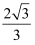 ,且S△ABF=1﹣
,且S△ABF=1﹣  .抛物线N的顶点在坐标原点,焦点为F.
.抛物线N的顶点在坐标原点,焦点为F.
 =1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e=
=1(a>0,b>0)的上焦点为F,上顶点为A,B为虚轴的端点,离心率e= 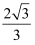 ,且S△ABF=1﹣
,且S△ABF=1﹣  .抛物线N的顶点在坐标原点,焦点为F.
.抛物线N的顶点在坐标原点,焦点为F.
-
(1) 求双曲线M和抛物线N的方程;
-
(2) 设动直线l与抛物线N相切于点P,与抛物线的准线相交于点Q,则以PQ为直径的圆是否恒过y轴上的一个定点?如果经过,试求出该点的坐标,如果不经过,试说明理由.
已知双曲线  的一个焦点与抛物线
的一个焦点与抛物线  的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于  ,则双曲线的方程为( )
,则双曲线的方程为( )
 的一个焦点与抛物线
的一个焦点与抛物线  的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于  ,则双曲线的方程为( )
,则双曲线的方程为( )
A .  B .
B .  C .
C .  D .
D . 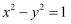
 B .
B .  C .
C .  D .
D . 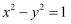
若双曲线  的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 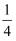 ,则该双曲线的虚轴长是( )
,则该双曲线的虚轴长是( )
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 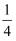 ,则该双曲线的虚轴长是( )
,则该双曲线的虚轴长是( )
A . 2
B . 1
C .  D .
D . 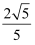
 D .
D . 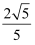
已知双曲线  (a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
 (a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
A . 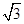 B .
B .  C .
C .  D .
D . 
已知双曲线 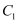 :
: 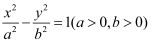 ,
,  :
: 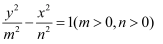 ,若双曲线
,若双曲线 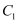 ,
,  的渐近线方程均为
的渐近线方程均为  ,且离心率分别为
,且离心率分别为 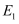 ,
, 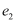 ,则
,则 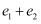 的最小值为
的最小值为 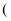
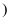
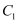 :
: 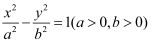 ,
,  :
: 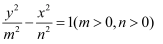 ,若双曲线
,若双曲线 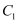 ,
,  的渐近线方程均为
的渐近线方程均为  ,且离心率分别为
,且离心率分别为 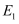 ,
, 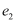 ,则
,则 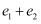 的最小值为
的最小值为 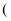
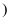
A . 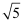 B .
B . 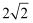 C .
C . 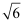 D .
D . 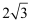
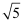 B .
B . 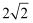 C .
C . 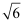 D .
D . 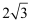
已知双曲线  :
: 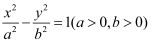 的右顶点为
的右顶点为  ,以
,以  为圆心,
为圆心,  为半径作圆
为半径作圆  ,圆
,圆  与双曲线
与双曲线  的一条渐近线于交
的一条渐近线于交  、
、  两点,若
两点,若  ,则
,则  的离心率为.
的离心率为.
 :
: 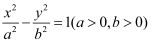 的右顶点为
的右顶点为  ,以
,以  为圆心,
为圆心,  为半径作圆
为半径作圆  ,圆
,圆  与双曲线
与双曲线  的一条渐近线于交
的一条渐近线于交  、
、  两点,若
两点,若  ,则
,则  的离心率为.
的离心率为.
已知  是双曲线
是双曲线  的右焦点,
的右焦点,  是
是  左支上一点,
左支上一点,  ),当
),当  周长最小时,则点
周长最小时,则点  的纵坐标为( )
的纵坐标为( )
 是双曲线
是双曲线  的右焦点,
的右焦点,  是
是  左支上一点,
左支上一点,  ),当
),当  周长最小时,则点
周长最小时,则点  的纵坐标为( )
的纵坐标为( )
A .  B .
B . 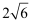 C .
C . 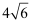 D .
D . 
 B .
B . 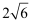 C .
C . 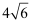 D .
D . 
已知  为双曲线:
为双曲线: 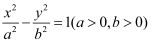 右支上一点,A为其左顶点,
右支上一点,A为其左顶点,  为其右焦点,满足
为其右焦点,满足  ,
,  ,则点F到直线
,则点F到直线 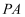 的距离为( )
的距离为( )
 为双曲线:
为双曲线: 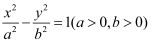 右支上一点,A为其左顶点,
右支上一点,A为其左顶点,  为其右焦点,满足
为其右焦点,满足  ,
,  ,则点F到直线
,则点F到直线 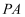 的距离为( )
的距离为( )
A . 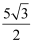 B .
B .  C .
C .  D .
D . 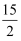
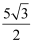 B .
B .  C .
C .  D .
D . 
如图为陕西博物馆收藏的国宝——唐⋅金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯的主体部分可以近似看作是双曲线  1(a>0,b>0)的右支与y轴及平行于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为
1(a>0,b>0)的右支与y轴及平行于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为  ,下底座外直径为
,下底座外直径为  ,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周长为( )
,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周长为( )
 1(a>0,b>0)的右支与y轴及平行于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为
1(a>0,b>0)的右支与y轴及平行于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为  ,下底座外直径为
,下底座外直径为  ,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周长为( )
,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周长为( ) 
A . 2  π
B . 3π
C . 2
π
B . 3π
C . 2  π
D . 4π
π
D . 4π
 π
B . 3π
C . 2
π
B . 3π
C . 2  π
D . 4π
π
D . 4π
已知双曲线  的左、右焦点分别为
的左、右焦点分别为 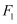 、
、  ,
,  是双曲线上一点,且
是双曲线上一点,且  轴,若
轴,若  的内切圆半径为
的内切圆半径为  ,则其渐近线方程是.
,则其渐近线方程是.
 的左、右焦点分别为
的左、右焦点分别为 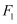 、
、  ,
,  是双曲线上一点,且
是双曲线上一点,且  轴,若
轴,若  的内切圆半径为
的内切圆半径为  ,则其渐近线方程是.
,则其渐近线方程是.
伦敦奥运会自行车赛车馆有一个明显的双曲线屋顶,该赛车馆是数学与建筑完美结合造就的艺术品,若将如图所示的双曲线屋顶的一段近似看成离心率为 的双曲线
的双曲线 上支的一部分,点F是C的下焦点,若点P为C上支上的动点,则
上支的一部分,点F是C的下焦点,若点P为C上支上的动点,则 与P到C的一条渐近线的距离之和的最小值为( )
与P到C的一条渐近线的距离之和的最小值为( )
 的双曲线
的双曲线 上支的一部分,点F是C的下焦点,若点P为C上支上的动点,则
上支的一部分,点F是C的下焦点,若点P为C上支上的动点,则 与P到C的一条渐近线的距离之和的最小值为( )
与P到C的一条渐近线的距离之和的最小值为( )

A . 2
B . 3
C . 4
D . 5
已知点 在双曲线
在双曲线 的右支上,
的右支上, , 动点
, 动点 满足
满足 ,
,  是双曲线的右焦点,则
是双曲线的右焦点,则 的最大值为.
的最大值为.
 在双曲线
在双曲线 的右支上,
的右支上, , 动点
, 动点 满足
满足 ,
,  是双曲线的右焦点,则
是双曲线的右焦点,则 的最大值为.
的最大值为.
已知双曲线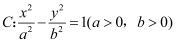 的左、右焦点分别为
的左、右焦点分别为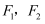 , 点
, 点 为线段
为线段 的中点,过
的中点,过 的直线
的直线 与
与 的右支交于
的右支交于 两点,延长
两点,延长 分别与
分别与 交于点
交于点 两点,若
两点,若 的离心率为
的离心率为 为
为 上一点.
上一点.
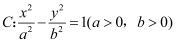 的左、右焦点分别为
的左、右焦点分别为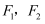 , 点
, 点 为线段
为线段 的中点,过
的中点,过 的直线
的直线 与
与 的右支交于
的右支交于 两点,延长
两点,延长 分别与
分别与 交于点
交于点 两点,若
两点,若 的离心率为
的离心率为 为
为 上一点.
上一点.
-
(1) 求证:
 ;
;
-
(2) 已知直线
 和直线
和直线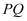 的斜率都存在,分别记为
的斜率都存在,分别记为 , 判断
, 判断 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
最近更新



