离散型随机变量的期望与方差 知识点题库
 , 则n的值为( )
, 则n的值为( )
甲地区:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 2 | 3 | 10 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 1 |
乙地区:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 9 | 8 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
(Ⅰ)计算x,y的值;
(Ⅱ)根据抽样结果分别估计甲地区和乙地区的优秀率;若将此优秀率作为概率,现从乙地区所有学生中随机抽取3人,求抽取出的优秀学生人数ξ的数学期望
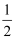 ,其余每局比赛甲队获胜的概率都是
,其余每局比赛甲队获胜的概率都是 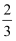 .设各局比赛结果相互独立.
.设各局比赛结果相互独立.
-
(1) 分别求甲队3:0,3:1,3:2胜利的概率;
-
(2) 若比赛结果3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分,对方得1分,求乙队得分X的分布列及数学期望.
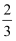 ,设甲投中蓝的次数为X,则期望E(X)=.
,设甲投中蓝的次数为X,则期望E(X)=.
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
 ,方差为s2 , 则( )
,方差为s2 , 则( )
 =5,s2>3
B .
=5,s2>3
B .  =5,s2<3
C .
=5,s2<3
C .  >5,s2<3
D .
>5,s2<3
D .  >5,s2>3
>5,s2>3

-
(1) 求某两人选择同一套餐的概率;
-
(2) 若用随机变量X表示某两人所获优惠金额的总和,求X的分布列和数学期望.
ξ | 7 | 8 | 9 | 10 |
P | x | 0.1 | 0.3 | y |
已知ξ的数学期望E(ξ)=8.9,则y的值为( ).
 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下: | 年龄 | | | | | |
| 支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |

-
(1) 由以上统计数据填
 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异; 45岁以下
45岁以上
总计
支持
不支持
总计
-
(2) 若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为
 ,求随机变量
,求随机变量  的分布列及数学期望.
的分布列及数学期望.
-
(1) 你能否估算出中学生早恋人数的百分比?
-
(2) 若从该地区中学生中随机抽取一个班(40人),设其中恰有
 个人存在早恋的现象,求
个人存在早恋的现象,求  的分布列及数学期望.
的分布列及数学期望.
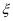 表示所选3人中女生的人数.
表示所选3人中女生的人数.
-
(1) 求所选3人中女生人数
 的概率;
的概率;
-
(2) 求
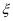 的分布列及数学期望.
的分布列及数学期望.
-
(1) 求挑选的2台电脑都是B品牌电脑的概率;
-
(2) 设挑选的2台电脑中A品牌的台数为X,求X的分布列和均值.
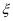 ,则
,则  ,
,  .
.
 列联表:
列联表: 
-
(1) 根据列联表,能否有
 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
-
(2) 若已经从40岁以上的被调查者中用分层抽样的方式抽取了10名,现从这10名被调查者中随机选取3名,记这3名被选出的被调查者中对手机游戏很有兴趣的人数为
 ,求
,求  的分布列及数学期望.
的分布列及数学期望. 附:

参考数据:

|
日照情况 |
日均气温不低于15℃ |
日均气温低于15℃ |
|
日照充足 |
耗电0千瓦时 |
耗电5千瓦时 |
|
日照不足 |
耗电5千瓦时 |
耗电10千瓦时 |
|
日照严重不足 |
耗电15千瓦时 |
耗电20千瓦时 |
根据调查,当地每天日照充足的概率为 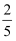 ,日照不足的概率为
,日照不足的概率为 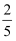 ,日照严重不足的概率为
,日照严重不足的概率为 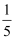 .2020年这一年的日均气温的频率分布直方图如图所示,区间分组为
.2020年这一年的日均气温的频率分布直方图如图所示,区间分组为  ,
,  ,
,  ,
,  ,
,  ,
,  .
.

-
(1) 求图中
 的值,并求一年中日均气温不低于15℃的频率;
的值,并求一年中日均气温不低于15℃的频率;
-
(2) 用频率估计概率,已知该工厂原来的电热水器平均每天耗电20千瓦时,试估计更换电辅式太阳能热水器后这一年能省多少电?(一年以365天计算)
|
日需求量杯数 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
天数 |
5 |
5 |
10 |
15 |
10 |
10 |
5 |
以60天记录的各需求量的频率作为各需求量发生的概率.
-
(1) 从这60天中任取2天,求这2天的日需求量至少有一天为35的概率;
-
(2) ①若奶茶店一天准备了35杯这款新品奶茶,用
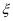 表示当天销售这款新品奶茶的利润(单位:元),求
表示当天销售这款新品奶茶的利润(单位:元),求 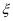 的分布列和数学期望;
的分布列和数学期望; ②假设奶茶店每天准备的这款新品奶茶倍数都是5的倍数,有顾客建议店主每天准备40杯这款新品奶茶,你认为店主应该接受这个建议吗?请说明理由.
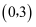 和
和  内分别选取一个实数
内分别选取一个实数  ,
, 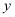 ,得到一个实数对
,得到一个实数对 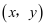 ,称为完成一次试验.若独立重复做3次试验,则
,称为完成一次试验.若独立重复做3次试验,则  的次数
的次数 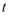 的数学期望为( )
的数学期望为( )
 B .
B . 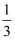 C .
C .  D .
D . 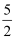
年份 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均存款y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
变量t,y具有线性相关关系.现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲 ;乙
;乙 ;丙
;丙 , 其中有且仅有一位同学的计算结果是正确的.
, 其中有且仅有一位同学的计算结果是正确的.
-
(1) 试判断谁的计算结果正确?
-
(2) 若由线性回归方程得到的估计数据与检测数据的误差大于0.1,则称该数据为“不可靠数据”,若误差为0,则称该检测数据是“完美数据”,这两者之外的其余数据均称为“可靠数据”.现剔除不可靠数据,从剩余数据中随机抽取2个,求其中“完美数据”个数的分布列和数学期望.
 的分布列如下表:
的分布列如下表:
|
|
1 |
2 |
3 |
4 |
5 |
|
|
m |
0.1 |
0.3 |
n |
0.3 |
若离散型随机变量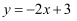 , 且
, 且 , 则正确的是( )
, 则正确的是( )
 B .
B .  C .
C .  D .
D . 









