21.2 解一元二次方程 知识点题库
若关于x的一元二次方程(m-1)x2-2x-1=0有两个实数根,则实数m的取值范围是( )
A . m≥0
B . m>0
C . m≥0且m≠1
D . m>0且m≠1
解方程:
-
(1) (2x﹣1)2=(x﹣3)2;
-
(2) x2﹣2
 x﹣1=0
x﹣1=0
关于x的一元二次方程x2+2x﹣m=0有实数根,则m的取值范围是( )
A . m≥﹣1
B . m>﹣1
C . m≤﹣1
D . m<﹣1
当x=时,代数式6x2+15x+12的值等于21.
已知:关于x的方程 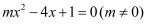 有实数根.
有实数根.
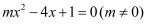 有实数根.
有实数根.
-
(1) 求m的取值范围;
-
(2) 若方程的根为有理数,求正整数m的值.
判断方程4x2﹣1=3x是否有解,如果有,请求出该方程的解;如果没有,请说明理由.
用配方法解方程:4x2+8x+3=0.
若一元二次方程x2﹣4x﹣4m=0有两个不等的实数根,则反比例函数y= 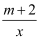 的图象所在的象限是( )
的图象所在的象限是( )
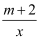 的图象所在的象限是( )
的图象所在的象限是( )
A . 第一、二象限
B . 第一、三象限
C . 第二、四象限
D . 第三、四象限
法国数学家弗朗索瓦·韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系,由于韦达最早发现代数方程的根与系数之间有这种关系,人们把这个关系称为韦达定理.它的内容如下:在一元二次方程 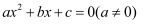 中,它的两根
中,它的两根 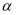 、
、 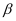 有如下关系:
有如下关系: 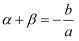 ,
, 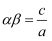 .
.
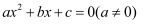 中,它的两根
中,它的两根 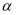 、
、 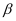 有如下关系:
有如下关系: 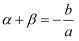 ,
, 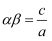 .
.
韦达定理还有逆定理,它的内容如下:如果两数 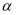 和
和 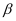 满足如下关系:
满足如下关系: 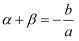 ,
, 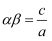 ,那么这两个数
,那么这两个数 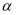 和
和 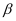 是方程
是方程 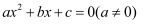 的根.通过韦达定理的逆定理,我们就可以利用两数的和积关系构造一元二次方程.例如:
的根.通过韦达定理的逆定理,我们就可以利用两数的和积关系构造一元二次方程.例如: 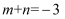 ,
, 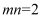 ,那么
,那么  和
和  是方程
是方程 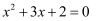 的两根.
的两根.
请应用上述材料解决以下问题:
-
(1) 已知
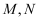 是两个不相等的实数,且满足
是两个不相等的实数,且满足 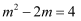 ,
, 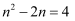 ,求
,求 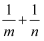 的值.
的值.
-
(2) 已知实数x,y满足
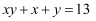 ,
,  ,求
,求  的值.
的值.
一元二次方程 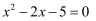 的根的情况是( )
的根的情况是( )
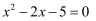 的根的情况是( )
的根的情况是( )
A . 有两个相等的实数根
B . 没有实数根
C . 有两个不相等的实数根
D . 无法确定
已知a、b、c是等腰△ABC的三边长,其中a=4,b和c是关于x的方程x2-mx+3m=0的两根,求m的值.
关于x的一元二次方程 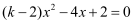 有两个不相等的实数根.
有两个不相等的实数根.
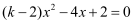 有两个不相等的实数根.
有两个不相等的实数根.
-
(1) 求k的取值范围;
-
(2) 如果符合条件的最大整数k是一元二次方程
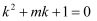 的根,求m的值.
的根,求m的值.
若关于x的一元二次方程ax2-2x+1=0有两个实数根,则实数a的取值范围是( )
A . a≤1且a≠0
B . a<1且a≠0
C . a≤1
D . a<1
阅读下列材料:定义任意两个实数a , b , 按规则p=ab﹣a+b扩充得到一个新数p , 称所得的新数p为a , b的“衍生数”.
-
(1) 若a=2,b=﹣3,则a , b的“衍生数”p=.
-
(2) 若a=﹣m﹣3,b=m , 求a , b的“衍生数”p的最大值.
解下列方程
-
(1)
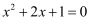
-
(2)

定义:cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程,下列四个结论中,错误的是( )
A . 如果x=2是×2+2x+c=0的倒方程的解,则c=  B . 如果ac<0,那么这两个方程都有两个不相等的实数根
C . 如果一元二次方程ax2-2x+c=0无解,则它的倒方程也无解
D . 如果一元二次方程ax2-2x+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
B . 如果ac<0,那么这两个方程都有两个不相等的实数根
C . 如果一元二次方程ax2-2x+c=0无解,则它的倒方程也无解
D . 如果一元二次方程ax2-2x+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
 B . 如果ac<0,那么这两个方程都有两个不相等的实数根
C . 如果一元二次方程ax2-2x+c=0无解,则它的倒方程也无解
D . 如果一元二次方程ax2-2x+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
B . 如果ac<0,那么这两个方程都有两个不相等的实数根
C . 如果一元二次方程ax2-2x+c=0无解,则它的倒方程也无解
D . 如果一元二次方程ax2-2x+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根
对任意一个四位数n,如果千位与十位上的数字之和为7,百位与个位上的数字之和也为7,那么称n为“上进数”.
-
(1) 写出最小和最大的“上进数”;
-
(2) 一个“上进数”
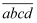 ,若
,若 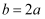 ,且使一元二次方程
,且使一元二次方程 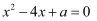 有两个不相等的实数根,求这个“上进数”.
有两个不相等的实数根,求这个“上进数”.
已知a、b、c为实数,且 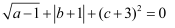 ,求方程ax2+bx+c=0的根.
,求方程ax2+bx+c=0的根.
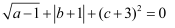 ,求方程ax2+bx+c=0的根.
,求方程ax2+bx+c=0的根.
已知x,y为有理数,且满足x2+4y2+6x﹣4y+10=0,求代数式yx的值.
对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a) 2的形式.但对于二次三项式x2+2ax-3a2 , 就不能直接运用公式了.此时,我们可以在二次三项式x2+2ax-3a2中先加上一项a2 , 使它与x2+2ax的和成为一个完全平方式,再减去a2 , 整个式子的值不变,于是有:x2+2ax-3a2= x2+2ax+a2- a2- 3a2=(x+a) 2- (2a)2=(x+3a) (x -a),像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.
-
(1) 利用“配方法”分解因式:
①x2-8x-9
② a4+a2b2+ b4
-
(2) 若a+ b=4,ab=2,求①a2+b2;②a4+b4的值.
-
(3) 已知x是任意实数,试比较
 与
与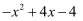 的大小,说明理由.
的大小,说明理由.
最近更新



