数学思想 知识点题库
已知a+b=3,  ,则
,则 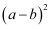 =
=
 ,则
,则 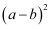 =
=
著名的斐波那契数列1、2、3、5、8、13、21、…,其中的第9个数是.
如图,已知直线y1:y=kx+b与直线y2:y=mx+n相交于P(﹣3,2),则关于x不等式mx+n≤kx+b的解集为( )

A . x≤﹣3
B . x≥﹣3
C . x≤2
D . x≥2
已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是.
对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB= 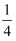 ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
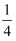 ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
-
(1) 当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是;
②点T在直线y=﹣
 x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围; -
(2) ⊙C的圆心在x轴上,半径为1,直线y=﹣2x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,请求出圆心C的横坐标n的取值范围.

《庄子》一书里有:“一尺之棰(木棍),日取其半,万世不竭(尽,完)”这句话可以用数学符号表示:1=  ;也可以用图形表示.上述研究问题的过程中体现的主要数学思想是( )
;也可以用图形表示.上述研究问题的过程中体现的主要数学思想是( )
 ;也可以用图形表示.上述研究问题的过程中体现的主要数学思想是( )
;也可以用图形表示.上述研究问题的过程中体现的主要数学思想是( ) 
A . 函数思想
B . 数形结合思想
C . 公理化思想
D . 分类讨论思想
如图,在Rt△ABC中,∠C=90°,AC=4,cosA= 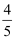 ,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为.
,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为.
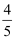 ,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为.
,点D是斜边AB上的动点且不与A,B重合,连接CD,点B'与点B关于直线CD对称,连接B'D,当B'D垂直于Rt△ABC的直角边时,BD的长为. 
在平面直角坐标系xOy中,抛物线 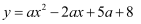 (
( 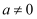 ).
).
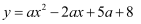 (
( 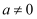 ).
). 
-
(1) 写出抛物线顶点的纵坐标(用含a的代数式表示);
-
(2) 若该抛物线与x轴的两个交点分别为点A和点B,且点A在点B的左侧,AB=4.
①求a的值;
②记二次函数图象在点A,B之间的部分为W(含点A和点B),若直线
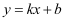 (
( 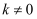 )经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
)经过(1,-1),且与图形W有公共点,结合函数图象,求b的取值范围.
如图, 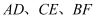 是
是 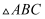 的高,
的高, 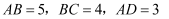 ,则
,则  .
.
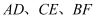 是
是 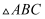 的高,
的高,  ,则
,则  .
. 
已知  是
是  的一条弦,点
的一条弦,点  在
在 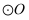 上,联结
上,联结 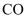 并延长,交弦
并延长,交弦  于点
于点  ,且
,且 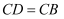 .
.
 是
是 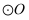 的一条弦,点
的一条弦,点  在
在 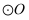 上,联结
上,联结 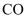 并延长,交弦
并延长,交弦  于点
于点  ,且
,且 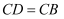 .
. 
-
(1) 如图1,如果
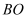 平分
平分 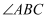 ,求证:
,求证: 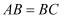 ;
; 
-
(2) 如图2,如果
 ,求
,求  的值;
的值;
-
(3) 延长线段
 交弦
交弦  于点
于点  ,如果
,如果  是等腰三角形,且
是等腰三角形,且 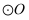 的半径长等于
的半径长等于 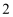 ,求弦
,求弦  的长.
的长.
如图所示,一次函数 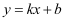 的图象与反比例函数
的图象与反比例函数 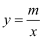 的图象交于
的图象交于  .
.
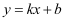 的图象与反比例函数
的图象与反比例函数 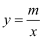 的图象交于
的图象交于  .
. 
-
(1) 求反比例函数和一次函数的解析式;
-
(2) 在x轴上存在一点C,使
 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
-
(3) 根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
如图,抛物线  的顶点为C,对称轴为直线
的顶点为C,对称轴为直线 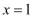 ,且经过点
,且经过点 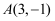 ,与y轴交于点B.
,与y轴交于点B.
 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线 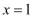 ,且经过点
,且经过点 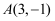 ,与y轴交于点B.
,与y轴交于点B. 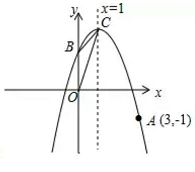
-
(1) 求抛物线的解析式;
-
(2) 连结
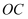 、
、  ,求
,求 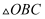 的面积;
的面积;
-
(3) 点
 是抛物线对称轴上一点,若
是抛物线对称轴上一点,若 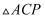 为等腰三角形,请直接写出所有点
为等腰三角形,请直接写出所有点  的坐标.
的坐标.
如图, 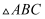 中,CD⊥AB,垂足为D,CD=BD=5,AD=4,点M从点B出发沿线段BA方向运动到点A停止,过点M作MN⊥AB,交折线BC﹣CA于点N,连接DN,AN,若
中,CD⊥AB,垂足为D,CD=BD=5,AD=4,点M从点B出发沿线段BA方向运动到点A停止,过点M作MN⊥AB,交折线BC﹣CA于点N,连接DN,AN,若 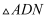 与
与  的面积相等,则线段BM的长为.
的面积相等,则线段BM的长为.
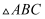 中,CD⊥AB,垂足为D,CD=BD=5,AD=4,点M从点B出发沿线段BA方向运动到点A停止,过点M作MN⊥AB,交折线BC﹣CA于点N,连接DN,AN,若
中,CD⊥AB,垂足为D,CD=BD=5,AD=4,点M从点B出发沿线段BA方向运动到点A停止,过点M作MN⊥AB,交折线BC﹣CA于点N,连接DN,AN,若 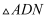 与
与  的面积相等,则线段BM的长为.
的面积相等,则线段BM的长为. 
在一个钝角三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“智慧三角形”.如,三个内角分别为120°,40°,20°的三角形是“智慧三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交射线OB于点C.

-
(1) ∠ABO的度数为°,△AOB(填“是”或“不是”) “智慧三角形”;
-
(2) 若∠OAC=20°,求证:△AOC为“智慧三角形”;
-
(3) 当△ABC为“智慧三角形”时,求∠OAC的度数.
等腰三角形的一边长是4,方程  的两个根是三角形的两边长,则m为( )
的两个根是三角形的两边长,则m为( )
 的两个根是三角形的两边长,则m为( )
的两个根是三角形的两边长,则m为( )
A . 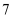 B .
B . 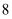 C .
C . 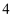 D . 7或8
D . 7或8
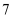 B .
B . 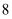 C .
C . 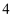 D . 7或8
D . 7或8
阅读下列材料,完成相应任务.
|
直角三角形斜边上的中线等于斜边的一半 如图1, 分析:要证明 |

-
(1) 请你按材料中的分析写出证明过程;
-
(2) 上述证明方法中主要体现的数学思想是______;A . 转化思想 B . 类比思想 C . 数形结合思想 D . 从一般到特殊思想
-
(3) 如图3,点
 是线段
是线段  上一点,
上一点, 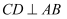 ,点
,点  是线段
是线段 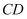 上一点,分别连接
上一点,分别连接 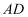 ,
, 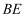 ,点
,点  ,
,  分别是
分别是 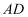 和
和 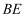 的中点,连接
的中点,连接 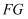 .若
.若 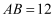 ,
, 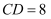 ,
,  .则
.则  .
.
老师布置了一道题:“已知A、B、C在同一直线上,AB=3cm,BC=1cm,求AC的长.”甲同学和乙同学分别给出了下列的解法一、解法二.
-
(1) 请认真阅读下列解法,并填空:
解法一:根据题意可分如下两种情形:
①C点在线段AB上;②C点在线段AB延长线上


AC==3-1=2(cm),AC==3+1=4(cm)
所以线段AC的长为2cm或4cm.
解法二:在直线AB上,以点A为原点,点A向右的方向为正方向,线段AB的长为3个单位长度建立如图所示的数轴.
则A:表示的数为0,B:表示的数为3;∵BC=1,∴点C表示的数为;所以线段AC的长为2cm或4cm.

-
(2) 丙同学学习了以上两种解法后若有所悟,觉得解法二很好,在解决线段的计算问题时,利用数形结合法比较简单.于是给同学们出了这样一道题:已知A、B、C、D在同一直线上,AB=3cm,BC=1cm,AD=1.5cm,求CD的长.请利用数形结合法解答丙同学的试题.

-
(3) 丁同学做完了丙同学的试题后,深受启发,觉得数形结合法太妙了,可以妙解点或线段的动态问题,于是编了以下试题:已知线段AB=3,线段CD在直线AB上运动,且CD=5,在运动的过程中,若点M、N分别为线段AC、BD的中点,求线段MN的长度.请用数形结合法解答丁同学的试题.

我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称之为“赵爽弦图”.现在勾股定理的证明已经有400多种方法,下面的两个图形就是验证勾股定理的两种方法,在验证著名的勾股定理过程,这种根据图形直观推论或验证数学规律和公式的方法,简称为 “无字证明”.在验证过程中它体现的数学思想是( )

A . 函数思想
B . 数形结合思想
C . 分类思想
D . 统计思想
平面直角坐标系是由原点重合且互相垂直的两条数轴构成的,它是沟通代数与几何的桥梁,是非常重要的数学工具.
-
(1) 最早引入坐标系,用代数方法研究几何图形的数学家是( )A . 祖冲之 B . 刘徽 C . 笛卡尔 D . 欧几里得
-
(2) 在数学活动课上,老师与同学们一起探究如下问题:
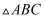 在平面直角坐标系中的位置如图,已知
在平面直角坐标系中的位置如图,已知 点的坐标为
点的坐标为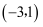 . 把
. 把 向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的
向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的 .
. 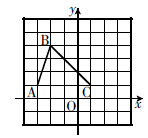
①写出点
 的坐标 ▲ ,
的坐标 ▲ , 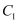 的坐标 ▲ ;
的坐标 ▲ ;②在
 轴上找一点
轴上找一点 , 使
, 使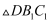 的面积等于3,求满足条件的点
的面积等于3,求满足条件的点 的坐标;
的坐标;③在解决问题②时用到的数学思想是 ▲ (填一个即可)
为了求n边形内角和,下面是老师与同学们从n边形的个顶点引出的对角线把n边形划分为若干个三角形,然后得出n边形的内角和公式.这种数学的推理方式是( )

A . 归纳推理
B . 数形结合
C . 公理化
D . 演绎推理
最近更新
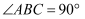 ,
, 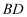 是斜边
是斜边 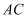 上的中线.求证:
上的中线.求证: 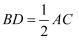 .
.
 .连接
.连接 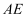 ,
, 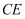 .可证四边形
.可证四边形  是矩形,由矩形的对角线相等得
是矩形,由矩形的对角线相等得  ,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到
,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到 


