数学思想 知识点题库
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.

-
(1) 问题:方程x3+x2﹣2x=0的解是x1=0,x2=,x3=;
-
(2) 拓展:用“转化”思想求方程
 =x的解;
=x的解;
-
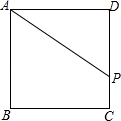
(3) 应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.

-
(1) 当P为AB的中点时,求DE的长及⊙M的半径;
-
(2) 当AM⊥DP时,求点P的坐标与⊙M的半径;
-
(3) 是否存在一点P使⊙M与矩形ABCO的另一条边也相切,若存在求出所有符合条件的点P的坐标.

-
(1) 求抛物线解析式;
-
(2) 当P点运动过程中满足PE=PD时,求此时点P的坐标;
-
(3) 如图2,从点B处沿着直线BC的垂线翻折PE得到FE',当点F在抛物线上时,求点P的坐标.

-
(1) 若P与B重合,当旋转角为时,这支铅笔与线段AB、AC围成的三角形是等腰三角形;
-
(2) 点P从B逐渐向A移动,记t=
 ,
, ①若t=1,当旋转角为30°、、、、210°、时这支铅笔与线段AB、AC共围成6个等腰三角形;
②当这支铅笔与线段AB、AC正好围成5个等腰三角形时,求t的取值范围;
③当这支铅笔与线段AB、AC正好围成3个等腰三角形时,直接写出t的取值范围.
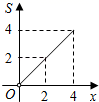 B .
B . 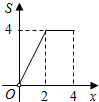 C .
C . 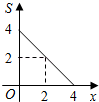 D .
D . 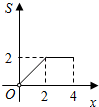
 中,抛物线
中,抛物线  与
与 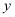 轴交于点A.
轴交于点A.
-
(1) 求点A的坐标(用含
 的式子表示);
的式子表示);
-
(2) 求抛物线与x轴的交点坐标;
-
(3) 已知点
 ,
,  ,如果抛物线与线段
,如果抛物线与线段  恰有一个公共点,结合函数图象,求a的取值范围.
恰有一个公共点,结合函数图象,求a的取值范围.
 ,则图中阴影部分面积为( )
,则图中阴影部分面积为( ) 
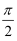 B . 2﹣
B . 2﹣ 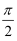 C . 2﹣π
D . 1﹣
C . 2﹣π
D . 1﹣ 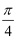
 是抛物线
是抛物线  (
(  为常数,
为常数,  )与x轴的一个交点.
)与x轴的一个交点.
-
(1) 当
 时,求该抛物线的顶点坐标;
时,求该抛物线的顶点坐标;
-
(2) 若抛物线与x轴的另一个交点为
 ,与y轴的交点为C , 过点C作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,
,与y轴的交点为C , 过点C作直线l平行于x轴,E是直线l上的动点,F是y轴上的动点,  .
. ①当点E落在抛物线上(不与点C重合),且
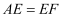 时,求点F的坐标;
时,求点F的坐标;②取
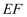 的中点N , 当m为何值时,
的中点N , 当m为何值时, 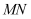 的最小值是
的最小值是 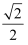 ?
?
 ,若∠BAC=90°,AB=AC=
,若∠BAC=90°,AB=AC=  ,则图中阴影部分的面积等于.
,则图中阴影部分的面积等于. 

 时,在方程两边同乘
时,在方程两边同乘 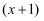 ,把原方程化为:2x-(x+1)=1,这一变形过程体现的数学思想主要是( )
,把原方程化为:2x-(x+1)=1,这一变形过程体现的数学思想主要是( )
 ,类似地,我们把
,类似地,我们把 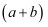 看成一个整体,则
看成一个整体,则  .“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
.“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.尝试应用:
-
(1) 把
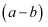 看成一个整体,合并
看成一个整体,合并  的结果是;
的结果是;
-
(2) 已知
 ,求
,求  的值;
的值;
-
(3) 已知
 ,
,  ,
,  ,求
,求  的值.
的值.

转化思想是常用的数学思想之一.在研究新问题或复杂问题时,常常把问题转化为熟悉的或比较简单的问题来解决.如解一元二次方程是转化成一元一次方程来解决的;解分式方程是转化为整式方程来解决的.由于“去分母”可能产生增根,所以解分式方程必须检验.
利用转化思想,我们还可以解一些新的方程,如无理方程(根号下含有未知数的方程).解无理方程关键是要去掉根号,可以将方程适当变形后两边同时平方,将其转化为整式方程.由于“去根号”可能产生增根,所以解无理方程也必须检验.
例如:解方程 
解:两边平方得: 
解得: 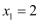 ,
, 
经检验, 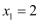 是原方程的根,
是原方程的根,
 代入原方程中不合理,是原方程的增根.
代入原方程中不合理,是原方程的增根.
∴原方程的根是 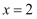 .
.
解决问题:
-
(1) 填空:已知关于x的方程
 有一个根是
有一个根是 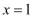 ,那么a的值为;
,那么a的值为;
-
(2) 求满足
 的x的值;
的x的值;
-
(3) 代数式
 的值能否等于8 ? 若能,求出
的值能否等于8 ? 若能,求出  的值;若不能,请说明理由.
的值;若不能,请说明理由.
 是以
是以  为直径的半圆上一点,连接
为直径的半圆上一点,连接 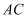 ,点
,点  是
是 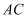 上一个动点,连接
上一个动点,连接  ,作
,作  交
交  于点
于点  ,交半圆于点
,交半圆于点  .已知:
.已知:  ,设
,设 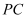 的长度为
的长度为 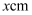 ,
,  的长度为
的长度为  ,
, 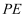 的长度为
的长度为  (当点
(当点  与点
与点  重合时,
重合时,  ,
,  ,当点
,当点  与点
与点  重合时,
重合时,  ,
,  ).
). 小锐同学根据学习函数的经验,分别对函数 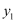 ,
, 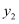 随自变量
随自变量  变化而变化的规律进行了探究.
变化而变化的规律进行了探究.

下面是小锐同学的探究过程,请补充完整:
-
(1) 按照下表中自变量
 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了 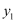 ,
, 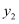 与
与  的几组对应值,请补全表格:
的几组对应值,请补全表格:  cm
cm0
1
2
3
4
5
6
7
8
 cm
cm8.00
5.81
4.38
3.35
2.55
1.85
1.21
0.60
0.00
 cm
cm0.00
0.90

2.24
2.67
2.89
2.83
2.34
0.00
上表中
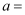 .(精确到0.1)
.(精确到0.1) -
(2) 在同一平面直角坐标系
 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点 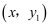 ,
,  ,并画出函数
,并画出函数 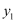 ,
, 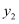 的图象(
的图象( 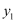 已经画出);
已经画出); 
-
(3) 结合函数图象解决问题:
①当
 ,
, 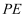 的长都大于
的长都大于 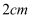 时,
时, 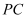 长度的取值范围约是 ▲ ;(精确到0.1)
长度的取值范围约是 ▲ ;(精确到0.1)②继续在同一坐标系中画出所需的函数图象,判断点
 ,
,  ,
,  能否在以
能否在以  为圆心的同一个圆上?(填“能”或“否”)
为圆心的同一个圆上?(填“能”或“否”)
 ,试求
,试求  的值.
的值. 解:设  ,则原方程变为
,则原方程变为  ,整理得
,整理得  ,即
,即  ,∴
,∴  .
.
∵  ,∴
,∴  .
.
上面这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
-
(1) 已知实数x , y满足
 ,求
,求  的值.
的值.
-
(2) 若四个连续正整数的积为120,求这四个连续正整数.
-
(1) 解方程:
 .
.
-
(2) 阅读下列材料,并完成相应任务.
三国时期的数学家赵爽在其所落的《勾股圆方图注》中记载了一元二次方程的几何解法,以
 为例,说明如下:
为例,说明如下:将方程
 变形为
变形为
 , 然后画四个长为
, 然后画四个长为
 , 宽为x的矩形,按如图所示的方式拼成一个“空心”大正方形.图中大正方形的面积可表示为
, 宽为x的矩形,按如图所示的方式拼成一个“空心”大正方形.图中大正方形的面积可表示为
 , 还可表示为四个矩形与一个边长为2的小正方形面积之和,即:
, 还可表示为四个矩形与一个边长为2的小正方形面积之和,即:
 ,
, 可得新方程:
 ,
, ∵x表示边长,
∴
 .
. ∴
 .
. 
任务一:①这种构造图形解一元二次方程的方法体现的数学思想是 ;
A.分类讨论思想 B.数形结合思想 C.演绎思想 D.公理化思想
②用配方法解方程:
 .
. 任务二:比较上述两种解一元二次方程的方法,请反思利用构造图形的方法求解一元二次方程的不足之处是 . (写出一条即可)



