分母有理化 知识点
把分母中的根号化去的过程称为分母有理化,具体做法如下:
1.
2.可通过类比分式中的“约分”进行分母有理化,如.
1.
2.可通过类比分式中的“约分”进行分母有理化,如.
分母有理化 知识点题库
已知 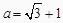 ,
, 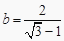 ,则a与b的关系为( ).
,则a与b的关系为( ).
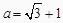 ,
, 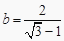 ,则a与b的关系为( ).
,则a与b的关系为( ).
A . a=b
B . ab=1
C . a=-b
D . ab=-1
化简: = .
= .
 = .
= .
与 ﹣2的乘积是有理数的是( )
﹣2的乘积是有理数的是( )
 ﹣2的乘积是有理数的是( )
﹣2的乘积是有理数的是( )
A .  ﹣2
B .
﹣2
B .  C . 2﹣
C . 2﹣ D .
D .  +2
+2
 ﹣2
B .
﹣2
B .  C . 2﹣
C . 2﹣ D .
D .  +2
+2
与2﹣ 相乘,结果是1的数为( )
相乘,结果是1的数为( )
 相乘,结果是1的数为( )
相乘,结果是1的数为( )
A .  B . 2-
B . 2- C . -2+
C . -2+ D . 2+
D . 2+
 B . 2-
B . 2- C . -2+
C . -2+ D . 2+
D . 2+
下列各式中正确的是( )
A . 3﹣2=﹣9
B . (72)3=75
C . x10÷x5=x2
D . 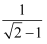 =
=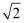 +1
+1
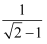 =
=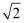 +1
+1
阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如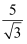 、
、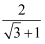 这样的式子,其实我们还可以将其进一步化简:
这样的式子,其实我们还可以将其进一步化简: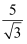 =
=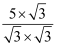 =
=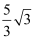 ;
;
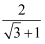 =
=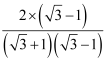 =
= =
= -1.以上这种化简过程叫做分母有理化.
-1.以上这种化简过程叫做分母有理化.
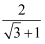 还可以用以下方法化简:
还可以用以下方法化简: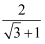 =
=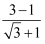 =
= =
=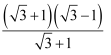 =
= -1.
-1.
(1)请用其中一种方法化简 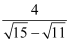 ;
;
(2)化简: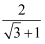 +
+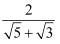 +
+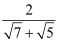 +...+
+...+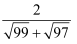 .
.
若a=2+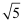 , b=
, b= , 那么a与b的关系是( )
, 那么a与b的关系是( )
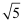 , b=
, b= , 那么a与b的关系是( )
, 那么a与b的关系是( )
A . a<b且互为相反数
B . a>b且a与b互为相反数
C . a>b
D . a=b
二次根式 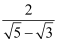 与
与 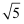 +
+ 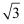 的关系是( )
的关系是( )
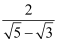 与
与 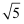 +
+ 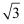 的关系是( )
的关系是( )
A . 互为相反数
B . 互为倒数
C . 互为有理化因式
D . 相等
在化简二次根式时,我们有时会碰上如 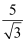 ,
,  ,
,  这样的式子,其实我们还可以将其进一步化简:
这样的式子,其实我们还可以将其进一步化简:
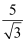 ,
,  ,
,  这样的式子,其实我们还可以将其进一步化简:
这样的式子,其实我们还可以将其进一步化简: 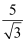 =
= 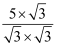 =
= 
 ;(一)
;(一)
 =
= 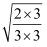 =
=  (二)
(二)
 =
= 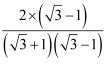 =
=  =
=  ﹣1(三)
﹣1(三)
以上这种化简的步骤叫做分母有理化.
 还可以用以下方法化简:
还可以用以下方法化简:
 =
=  =
=  =
= 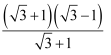 =
=  ﹣1(四)
﹣1(四)
-
(1) 参照阅读材料化简
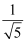 =
=
-
(2) 参照阅读材料化简
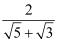 =
=
-
(3) 化简:
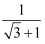 +
+  +
+ 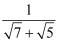 +…+
+…+ 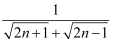 (n≥1,且n为整数).(直接写出结果即可)
(n≥1,且n为整数).(直接写出结果即可)
M= 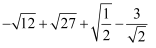 ,N=
,N=  ,
,
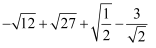 ,N=
,N=  ,
,
-
(1) 求M−N的值.
-
(2) 求
 的值;
的值;
-
(3) M N(填“>”“=”“< ”填空)
阅读下列解题过程:
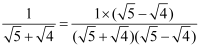 =
=  =
= 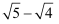 =
= 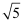 -2;
-2;
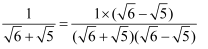 =
=  =
= 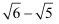 .
.
请回答下列问题:
-
(1) 观察上面的解题过程,请直接写出式子
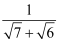 =;
=;
-
(2) 观察上面的解题过程,请直接写出式子
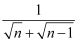 =;
=;
-
(3) 利用上面所提供的解法,请求
 +···+
+···+ 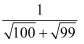 的值.
的值.
已知 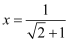 ,
, 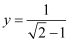 ,分别求下列代数式的值;
,分别求下列代数式的值;
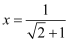 ,
, 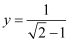 ,分别求下列代数式的值;
,分别求下列代数式的值;
-
(1)
 ;
;
-
(2)
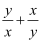 .
.
在将式子 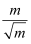 (m>0)化简时,
(m>0)化简时,
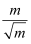 (m>0)化简时,
(m>0)化简时, 小明的方法是: 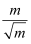 =
= 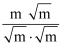 =
= 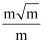 =
= 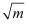 ;
;
小亮的方法是:  ;
;
小丽的方法是:  .
.
则下列说法正确的是( )
A . 小明、小亮的方法符合题意,小丽的方法不符合题意
B . 小明、小丽的方法符合题意,小亮的方法不符合题意
C . 小明、小亮、小丽的方法都符合题意
D . 小明、小丽、小亮的方法都不符合题意
-
(1) 观察下列各式的特点:
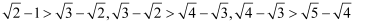 ,…根据以上规律可知
,…根据以上规律可知  .(填不等号)
.(填不等号)
-
(2) 观察下列式子的化简过程:
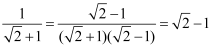 ,
, 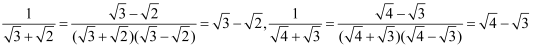 ,…根据观察,请写出式子
,…根据观察,请写出式子 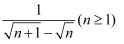 的化简过程.
的化简过程.
-
(3) 计算下列算式:
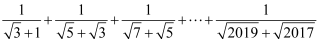
阅读材料
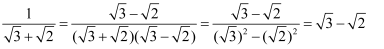 ,像上述解题过程中,
,像上述解题过程中, 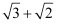 和
和 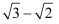 相乘的积不含二次根式,我们可以将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化。
相乘的积不含二次根式,我们可以将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化。
-
(1) 化简
①
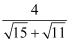 ;
;②
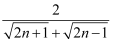 (n为整数);
(n为整数); -
(2) 化简:
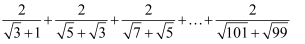
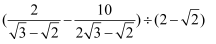
阅读下列材料,我们知道 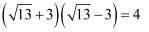 ,因此将
,因此将 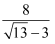 的分子分母同时乘以“
的分子分母同时乘以“ 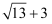 ”,分母就变成了4,即
”,分母就变成了4,即 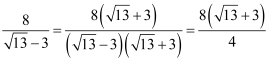 ,从而可以达到对根式化简的目的,根据上述阅读材料解决问题:若
,从而可以达到对根式化简的目的,根据上述阅读材料解决问题:若  ,则代数式m5+2m4﹣2017m3+2016的值是.
,则代数式m5+2m4﹣2017m3+2016的值是.
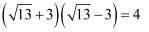 ,因此将
,因此将 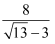 的分子分母同时乘以“
的分子分母同时乘以“ 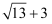 ”,分母就变成了4,即
”,分母就变成了4,即 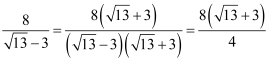 ,从而可以达到对根式化简的目的,根据上述阅读材料解决问题:若
,从而可以达到对根式化简的目的,根据上述阅读材料解决问题:若  ,则代数式m5+2m4﹣2017m3+2016的值是.
,则代数式m5+2m4﹣2017m3+2016的值是.
阅读下述材料:
我们在学习二次根式时,熟悉的分母有理化以及应用.其实,有一个类似的方法叫做“分子有理化”:
与分母有理化类似,分母和分子都乘以分子的有理化因式,从而消掉分子中的根式.比如: 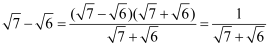
分子有理化可以用来比较某些二次根式的大小,也可以用来处理一些二次根式的最值问题.例如:比较 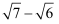 和
和 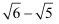 的大小.可以先将它们分子有理化.如下:
的大小.可以先将它们分子有理化.如下: 
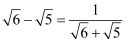
因为 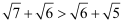 ,所以
,所以 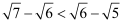
再例如:求 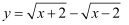 的最大值.做法如下:
的最大值.做法如下:
解:由 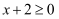 ,
, 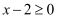 可知
可知 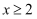 ,而
,而 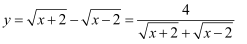
当 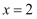 时,分母
时,分母 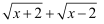 有最小值
有最小值 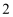 ,所以y的最大值是
,所以y的最大值是 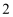 .
.
解决下述问题:
-
(1) 比较
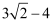 和
和 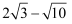 的大小;
的大小;
-
(2) 求
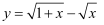 的最大值.
的最大值.
已知  +
+  +
+ 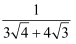 +…+
+…+ 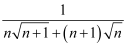 =
= 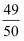 ,求n的值.
,求n的值.
 +
+  +
+ 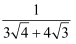 +…+
+…+ 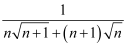 =
= 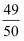 ,求n的值.
,求n的值.
小明在解决问题:已知a= 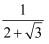 ,求2a2﹣8a+1的值,他是这样分析与解答的:
,求2a2﹣8a+1的值,他是这样分析与解答的:
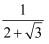 ,求2a2﹣8a+1的值,他是这样分析与解答的:
,求2a2﹣8a+1的值,他是这样分析与解答的: ∵a= 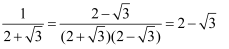 .
.
∴a﹣2=﹣  .
.
∴(a﹣2)2=3,即a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
-
(1) 计算:
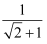 =;
=;
-
(2) 计算:
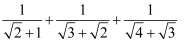 +…+
+…+ 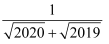 ;
;
-
(3) 若a=
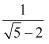 ,求2a2﹣8a+1的值.
,求2a2﹣8a+1的值.
最近更新



