勾股定理的应用 知识点题库
某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6 m、8 m.现要将其扩建成等腰三角形,且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.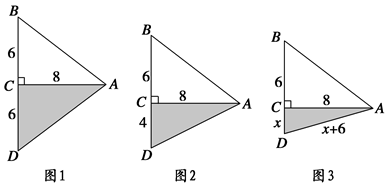
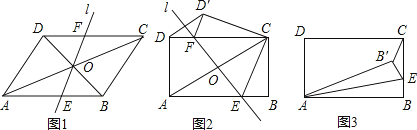
(1)如图1,在平行四边形ABCD中,对角线AC、BD相交于O点,过点O的直线l与边AB、CD分别交于点E、F,绕点O旋转直线l,猜想直线l旋转到什么位置时,四边形AECF是菱形.证明你的猜想.
(2)若将(1)中四边形ABCD改成矩形ABCD,使AB=4cm,BC=3cm,
①如图2,绕点O旋转直线l与边AB、CD分别交于点E、F,将矩形ABCD沿EF折叠,使点A与点C重合,点D的对应点为D′,连接DD′,求△DFD′的面积.
②如图3,绕点O继续旋转直线l,直线l与边BC或BC的延长线交于点E,连接AE,将矩形ABCD沿AE折叠,点B的对应点为B′,当△CEB′为直角三角形时,求BE的长度.请直接写出结果,不必写解答过程.
小华和小红都从同一点O出发,小华向北走了9米到A点,小红向东走了12米到了B点,则AB为 米.
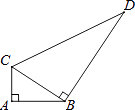
一个零件的形状如图所示,已知AC=3cm,AB=4cm,BD=12cm,求CD的长.
已知直线l1:y=﹣  与直线l2:y=kx﹣
与直线l2:y=kx﹣ 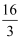 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
 与直线l2:y=kx﹣
与直线l2:y=kx﹣ 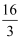 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.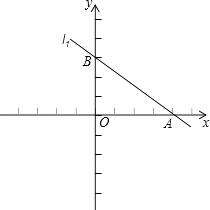
-
(1) 求k的值,并作出直线l2图象;
-
(2) 若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
-
(3) 若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由.
如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.

-
(1) 求证:直线BD与⊙O相切;
-
(2) 若AD:AE=4:5,BC=6,求⊙O的直径.
如图,△ABC中,∠ACB=90°,AC=24,BC=7,点M, N在AB上,且AM=AC, BN=BC,则MN的长为( )

A . 4
B . 5
C . 6
D . 7
在Rt△ ABC 中,∠ C =90°, BC ∶ AC =3∶4, AB =10,则 BC =, AC = .
已知两线段长分别为6cm,10cm,则当第三条线段长为cm时,这三条线段能组成直角三角形.
如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?

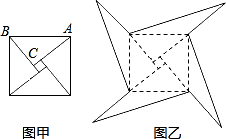
图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,面积为74的正方形.在Rt△ABC中,若直角边BC=5,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到图乙所示的“数学风车”.
-
(1) 这个风车至少需要绕着中心旋转才能和本身重合;
-
(2) 求这个风车的外围周长(图乙中的实线).
若△ABC的三边分别为5、12、13,则△ABC的面积是( )
A . 30
B . 40
C . 50
D . 60
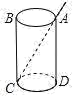
如图,有一个透明的直圆柱状的玻璃杯,现测得内径为 5cm,高为 12cm,今有一支 14cm 的吸 管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为.
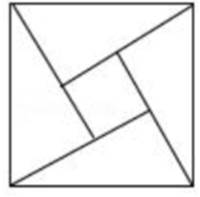
最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽.赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的.设直角三角形的两直角边长为a,b,且满足(a+b)2=23,若小正方形的面积为11,则大正方形的面积为( )
A . 15
B . 17
C . 30
D . 34
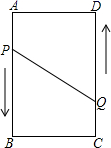
如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问P,Q两点从出发经过几秒时,点P,Q间的距离是10cm?
综合与实践:
问题情境:矩形旋转中的数学
已知在矩形  中,
中, 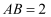 ,
, 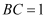 ,以点
,以点  为旋转中心,逆时针旋转矩形
为旋转中心,逆时针旋转矩形  ,旋转角为
,旋转角为  ,得到矩形
,得到矩形 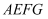 ,点
,点  、点
、点  、点
、点  的对应点分别为点
的对应点分别为点  、点
、点  、点
、点  .
.


-
(1) 操作猜想:如图①,当点
 落在
落在  边上时,求线段
边上时,求线段 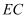 的长度;
的长度;
-
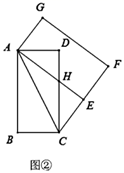
(2) 深入探究:如图②,当点
 落在线段
落在线段 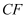 上时,
上时, 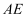 与
与  相交于点
相交于点 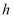 ,连接
,连接 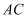 ,求线段
,求线段 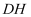 的长度;
的长度;
-
(3) 请从 A , B 两题中任选一题作答,我选 题.
A 题:如图③,设点
 为边
为边 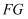 的中点,连接
的中点,连接  ,
, 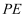 ,
, 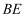 ,在矩形
,在矩形  旋转过程中,
旋转过程中,  的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
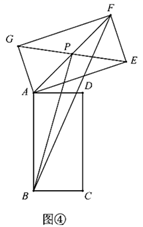
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.B 题:如图④,设点
 为矩形
为矩形 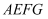 对角线交点,连接
对角线交点,连接  ,
, 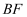 ,在矩形
,在矩形  旋转过程中,
旋转过程中,  的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
如图,网格中每个小正方形的边长均为1,点  ,
,  ,
,  都在格点上,以
都在格点上,以  为圆心,
为圆心,  为半径画弧,交最上方的网格线于点
为半径画弧,交最上方的网格线于点  ,则
,则 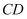 的长为( )
的长为( )
 ,
,  ,
,  都在格点上,以
都在格点上,以  为圆心,
为圆心,  为半径画弧,交最上方的网格线于点
为半径画弧,交最上方的网格线于点  ,则
,则 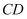 的长为( )
的长为( ) 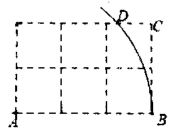
A .  B . 0.8
C .
B . 0.8
C . 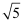 D .
D . 
 B . 0.8
C .
B . 0.8
C . 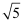 D .
D . 
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为16,则小正方形的面积为( )

A . 8
B . 6
C . 4
D . 3
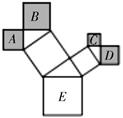
如图,一株美丽的勾股树如图所示,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A , B , C , D的面积分别为4,7,2,3,则最大的正方形E的面积是.
《九章算术》卷九中记载:今有立木,系索其末,委地三尺.引索却行,去本八尺而索尽.问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺.牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽.问绳索长是多少?
最近更新



