二次函数的实际应用-几何问题 知识点题库
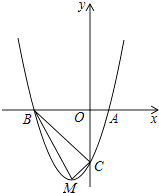
如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
-
(1) 求抛物线的函数表达式;
-
(2) 判断△BCM是否为直角三角形,并说明理由.
-
(3) 抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
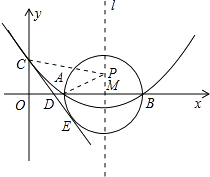
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ 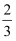 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
-
(1) 求抛物线的解析式及A、B两点的坐标;
-
(2) 在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
-
(3) 以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
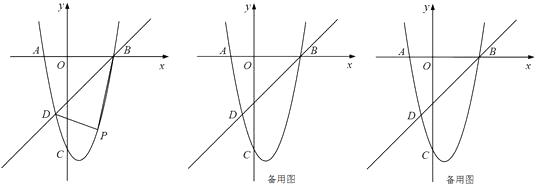
如图所示,已知抛物线经过点A(-2,0)、B(4,0)、C(0,-8),抛物线y=ax2+bx+c(a≠0)与直线y=x-4交于B , D两点.
-
(1) 求抛物线的解析式并直接写出D点的坐标;
-
(2) 点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标;
-
(3) 点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F , 交抛物线于点G . 当△QDG为直角三角形时,求点Q的坐标.
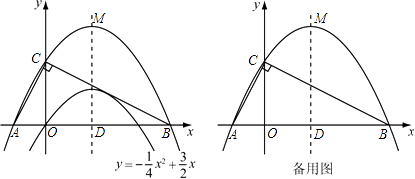
已知二次函数  的图象如图.
的图象如图.
-
(1) 求它的对称轴与x轴交点D的坐标;
-
(2) 将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
-
(3) 设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
在平面直角坐标系xOy中(如图).已知抛物线y=﹣  x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0, 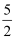 ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
 x2+bx+c经过点A(﹣1,0)和点B(0,
x2+bx+c经过点A(﹣1,0)和点B(0, 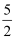 ),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
),顶点为C,点D在其对称轴上且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.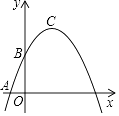
-
(1) 求这条抛物线的表达式;
-
(2) 求线段CD的长;
-
(3) 将抛物线平移,使其顶点C移到原点O的位置,这时点P落在点E的位置,如果点M在y轴上,且以O、D、E、M为顶点的四边形面积为8,求点M的坐标.
用长为6m的铝合金型材做一个形状如图所示的矩形窗框,要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成( )

A . 1.5m,1m
B . 1m,0.5m
C . 2m,1m
D . 2m,0.5m
两个等腰直角三角形如图放置,∠B=∠CAD=90°,AB=BC= 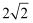 cm,AC=AD,垂直于CD的直线a从点C出发,以每秒
cm,AC=AD,垂直于CD的直线a从点C出发,以每秒  cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
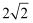 cm,AC=AD,垂直于CD的直线a从点C出发,以每秒
cm,AC=AD,垂直于CD的直线a从点C出发,以每秒  cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).
cm的速度沿CD方向匀速平移,与CD交于点E,与折线BAD交于点F;与此同时,点G从点D出发,以每秒1cm的速度沿着DA的方向运动;当点G落在直线a上,点G与直线a同时停止运动;设运动时间为t秒(t>0).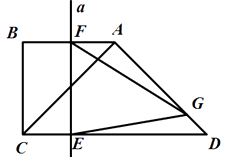

-
(1) 填空:CD=cm;
-
(2) 连接EG、FG,设△EFG的面积为y,求y与t之间的函数关系式,并写出相应t的取值范围;
-
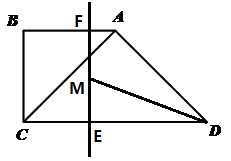
(3) 是否存在某一时刻t(0<t<2),作∠ADC的平分线DM交EF于点M,是否存在点M是EF的中点?若存在,求此时的t值;若不存在,请说明理由。
如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB= 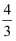 .
.
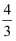 .
. 
-
(1) 则 A、B 两点的坐标分别为 A(,); B(,);
-
(2) 求这个二次函数的解析式;
-
(3) 在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为.
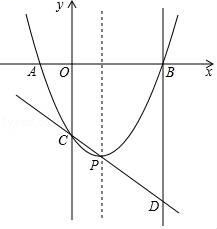
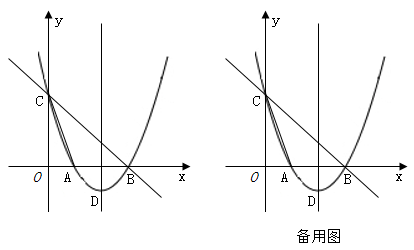
如图,在平面直角坐标系中,直线 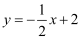 与x轴交于点A,与y轴交于点B,抛物线
与x轴交于点A,与y轴交于点B,抛物线  经过A,B两点且与x轴的负半轴交于点C.
经过A,B两点且与x轴的负半轴交于点C.
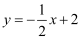 与x轴交于点A,与y轴交于点B,抛物线
与x轴交于点A,与y轴交于点B,抛物线  经过A,B两点且与x轴的负半轴交于点C.
经过A,B两点且与x轴的负半轴交于点C. 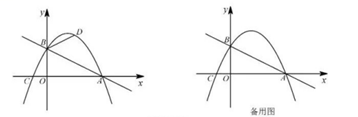
-
(1) 求该抛物线的解析式;
-
(2) 若点D为直线AB上方抛物线上的一个动点,当∠ABD=2∠BAC时,求点D的坐标;
-
(3) 已知E,F分别是直线AB和抛物线上的动点,当B,O,E,F为顶点的四边形是平行四边形时,直接写出所有符合条件的E点的坐标.
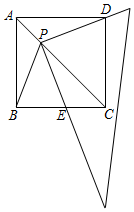
如图,一直角三角形的直角顶点P在边长为1的正方形ABCD对角线AC上运动(点P与A、C两点不重合)且它的一条直角边始终经过点D,另一直角边与射线BC交于点E.
-
(1) 当点E在BC边上时,
①求证:△PBC≌△PDC;
②判断△PBE的形状,并说明理由;
-
(2) 设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
如图,在平面直角坐标系中,已知 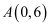 ,
, 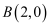 ,
, 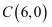 ,
,  为线段
为线段  上的动点,以
上的动点,以 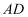 为边向右侧作正方形
为边向右侧作正方形 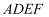 ,连接
,连接 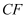 交
交 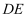 于点
于点  ,则
,则 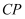 的最大值.
的最大值.
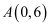 ,
, 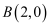 ,
, 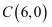 ,
,  为线段
为线段  上的动点,以
上的动点,以 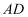 为边向右侧作正方形
为边向右侧作正方形 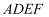 ,连接
,连接 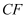 交
交 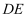 于点
于点  ,则
,则 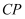 的最大值.
的最大值. 
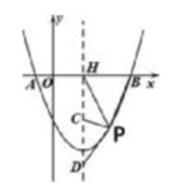
已知抛物线y=x2-2x-m+1(m为常数,m>0)与x轴交于A、B两点(点B在点A的右侧),点P为抛物线在第四象限上的一点,抛物线的对称轴与x轴交于点H,点D在对称轴上,PD=m,取HD的中点C,连结CP、BP,若PH平分∠BPC,BP=2PC,则m的值是( )
A . 1
B . 2
C . 3
D . 4
如图,在平面直角坐标系xOy中,抛物线y=ax²+bx+c与x轴交于点A(2,0)、B(6,0),与y轴交于点C(0,6),顶点为D,连结AC,作直线BC,点E是抛物线对称轴上的一个动点。
-
(1) 求出抛物线的解析式。
-
(2) 若∠BCE=∠OCA,求点E的坐标。
-
(3) 在(2)的条件下,延长CE交抛物线于点F,直接写出所有满足△GBD∽△FBC的点G的坐标。
长方形的周长为24cm,其中一边为xcm(其中 x>0),面积为  ,则这样的长方形中y与x的关系可以写为( )
,则这样的长方形中y与x的关系可以写为( )
 ,则这样的长方形中y与x的关系可以写为( )
,则这样的长方形中y与x的关系可以写为( )
A . 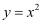 B .
B . 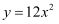 C .
C . 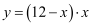 D .
D . 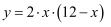
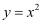 B .
B . 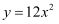 C .
C . 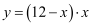 D .
D . 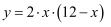
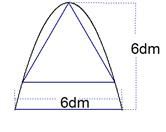
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到 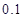 ,
, 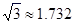 ).
).
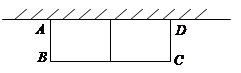
如图,有长为24米的篱笆,一面利用墙(图中的阴影部分就是墙,墙的最大可利用长度为9米),围成中间隔有一道篱笆的长方形花圃. 花圃的宽AB为x米,面积为S平方米.

-
(1) 求S与x的函数关系式及自变量x的取值范围;
-
(2) 当x为多少时,围成的花圃面积最大?最大面积是多少?
如图,在平面直角坐标系xOy中,抛物线L1:y=  +bx+c过点C(0,−3),与抛物线L2:y=−
+bx+c过点C(0,−3),与抛物线L2:y=−  −
− 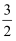 x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点.
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点.
 +bx+c过点C(0,−3),与抛物线L2:y=−
+bx+c过点C(0,−3),与抛物线L2:y=−  −
− 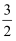 x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点.
x+2的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、L2上的动点. 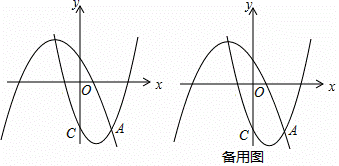
-
(1) 求抛物线L1对应的函数表达式;
-
(2) 若以点A.C. P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
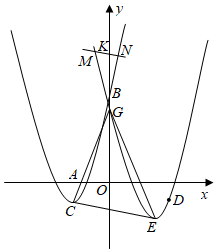
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(﹣1,0),B(0,3),顶点为C.平移此抛物线,得到一条新的抛物线,且新抛物线上的点D(3,﹣1)为原抛物线上点A的对应点,新抛物线顶点为E,它与y轴交于点G,连接CG,EG,CE.
-
(1) 求原抛物线对应的函数表达式;
-
(2) 在原抛物线或新抛物线上找一点F,使以点C,E,F,G为顶点的四边形是平行四边形,并求出点F的坐标;
-
(3) 若点K是y轴上的一个动点,且在点B的上方,过点K作CE的平行线,分别交两条抛物线于点M,N,且点M,N分别在y轴的两侧,当MN=CE时,请直接写出点K的坐标.
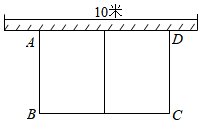
如图,某小区决定要在一块一边靠墙(墙长10米)的空地上用栅栏围成一个矩形绿化带ABCD,绿化带的一边靠墙,中间用栅栏隔成两个小矩形,所用栅栏总长为36米,设AB的长为x米,矩形绿化带的面积为S平方米.
-
(1) 求S与x之间的函数关系式,并直接写出x的取值范围;
-
(2) 求围成矩形绿化带ABCD面积S的最大值.
已知AB = BC,∠ABC = 90°,直线l是过点B的一条动直线(不与直线AB,BC重合),分别过点A,C作直线l的垂线,垂足为D,E.
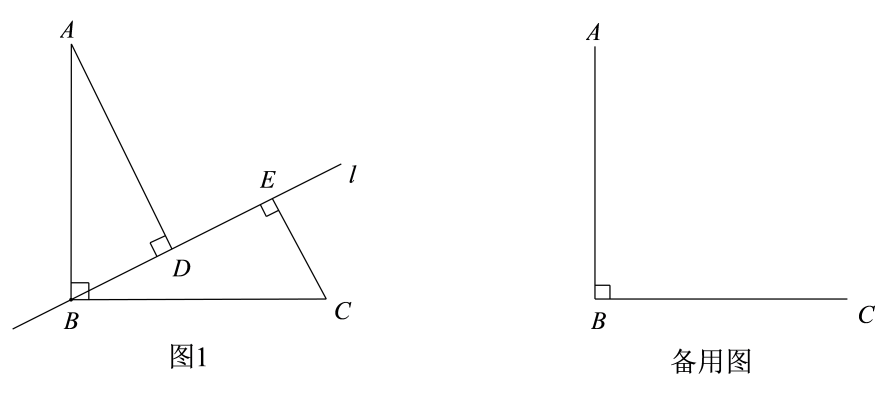
-
(1) 如图1,当45°<∠ABD<90°时,
①求证:CE +DE =AD;
②连接AE,过点D作DH⊥AE于H,过点A作AF∥BC交DH的延长线于点F.依题意补全图形,用等式表示线段DF,BE,DE的数量关系,并证明;
-
(2) 在直线l运动的过程中,若DE的最大值为3,直接写出AB的长.
最近更新



