第四章 基本平面图形 知识点题库
 ,以点
,以点  为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交  ,
,  于
于  ,
,  两点;分别以
两点;分别以  ,
,  为圆心,以大于
为圆心,以大于 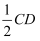 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点  ;以
;以  为端点作射线
为端点作射线 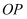 ,在射线
,在射线 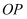 上截取线段
上截取线段 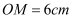 ,则射线
,则射线  上与点
上与点  的距离为
的距离为 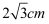 的点有( )
的点有( ) 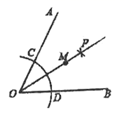
 .
. 
-
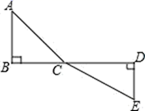
(1) 用含
 的代数式表示AC+CE的值;
的代数式表示AC+CE的值;
-
(2) 请问点C满足条件时,AC+CE的值最小,此时最小值为;
-
(3) 根据(2)中的结论,画图并标上数据,求代数式
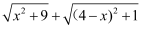 的最小值.
的最小值.
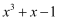 是三次三项式;④两点确定一条直线.其中正确的有( )
是三次三项式;④两点确定一条直线.其中正确的有( )
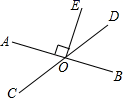
 与射线
与射线 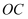 相交于点
相交于点  .
.
-
(1) 如图,
 ,射线
,射线 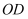 平分
平分 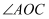 ,求
,求 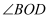 的度数;
的度数; 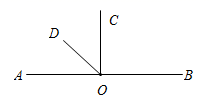
-
(2) 如图,
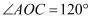 ,射线
,射线 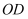 在
在 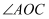 的内部,射线
的内部,射线 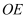 在
在 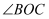 的内部,且
的内部,且  ,
, 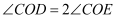 .若射线
.若射线 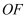 使
使 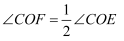 ,请在图中作出射线
,请在图中作出射线 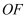 ,并求出
,并求出  的度数.
的度数. 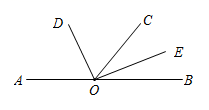
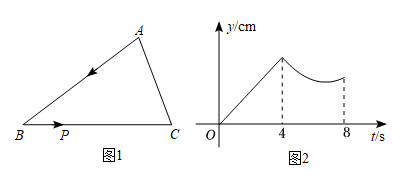
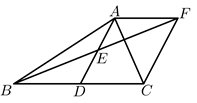
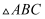 中,
中, 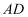 是
是  边上的中线,E是
边上的中线,E是 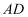 的中点,过点A作
的中点,过点A作 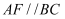 交
交 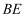 的延长线于点F,连结
的延长线于点F,连结 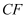 .
. 
-
(1) 求证:
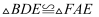 .
.
-
(2) 当
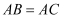 时,求证:四边形
时,求证:四边形 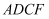 是矩形.
是矩形.
-
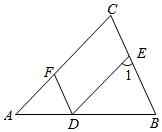
(1) 试说明:DF∥BC;
-
(2) 若∠1=70°,DF平分∠ADE , 求∠B的度数.
-
(1) 古希腊七贤之一,著名哲学家泰勒斯(Thales , 公元前6世纪)最早从拼图实践中发现了“三角形内角和等于
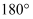 ”,但这种发现完全是经验性的,泰勒斯并没有给出严格的证明.之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明.其中欧几里得利用辅助平行线和延长线,通过一组同位角和内错角证明了该定理.请同学们帮助欧几里得将证明过程补充完整.
”,但这种发现完全是经验性的,泰勒斯并没有给出严格的证明.之后古希腊数学家毕达哥拉斯、欧几里得、普罗科拉斯等相继给出了基于平行线性质的不同的证明.其中欧几里得利用辅助平行线和延长线,通过一组同位角和内错角证明了该定理.请同学们帮助欧几里得将证明过程补充完整. 已知:如图,在
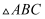 中,
中,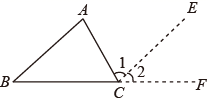
求证:
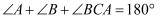 .
.证明:延长线段
 至点
至点  ,并过点
,并过点  作
作 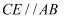 .
.∵
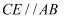 (已作),
(已作),∴ ▲
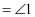 (两直线平行,内错角相等),
(两直线平行,内错角相等),▲
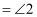 (两直线平行,同位角相等).
(两直线平行,同位角相等).∵ ▲ (平角的定义),
∴
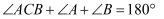 (等量代换).
(等量代换). -
(2) (实践运用)如图1,线段
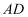 、
、  相交于点
相交于点  ,连结
,连结  、
、 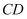 ,试证明:
,试证明: 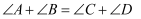 .
. 证明:
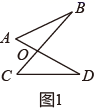
-
(3) (变化拓展)
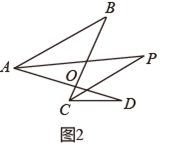
①如图2,
 、
、  分别平分
分别平分 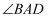 、
、 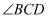 ,若
,若 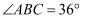 ,
, 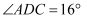 ,则
,则 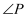 的度数为
的度数为  ;
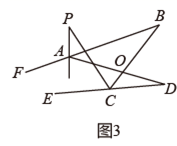
;②如图3,直线
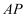 平分
平分 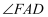 ,
, 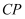 平分
平分 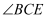 ,若
,若 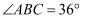 ,
, 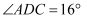 ,则
,则 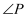 的度数为
的度数为  .
.

-
(1) 【理解】
如图1,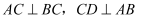 ,垂足分别为C、D,E是
,垂足分别为C、D,E是  的中点,连接
的中点,连接 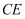 .已知
.已知 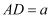 ,
, 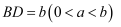 .
.
①分别求线段
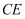 、
、 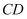 的长(用含a、b的代数式表示);
的长(用含a、b的代数式表示);②比较大小:
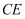 ▲
▲ 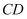 (填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系. -
(2) 【应用】
如图2,在平面直角坐标系 中,点M、N在反比例函数
中,点M、N在反比例函数 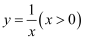 的图象上,横坐标分别为m、n.设
的图象上,横坐标分别为m、n.设 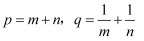 ,记
,记 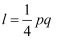 .
.
①当
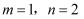 时,
时, 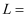 ▲ ;当
▲ ;当  时, ▲ ;
时, ▲ ;②通过归纳猜想,可得l的最小值是 ▲ .请利用图2构造恰当的图形,并说明你的猜想成立.
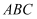 中,
中, 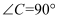 ,
, 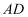 平分
平分 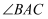 交
交  于点
于点  ,
, 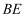 平分
平分 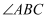 交
交 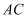 于点
于点  ,
, 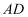 、
、 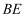 相交于点
相交于点  ,过点
,过点  作
作 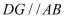 ,过点
,过点  作
作 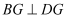 交
交 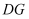 于点
于点  .下列结论:①
.下列结论:① 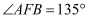 ;②
;②  ;③
;③  平分
平分  ;④
;④  .其中正确的是.
.其中正确的是. 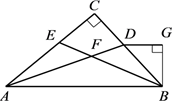
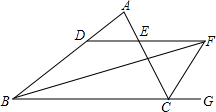
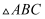 中,
中, 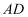 是
是  边上的高线,
边上的高线, 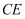 平分
平分 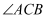 ,且
,且 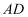 ,
, 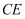 相交于点F,若
相交于点F,若 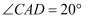 ,
, 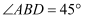 ,求
,求 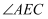 的度数.
的度数. 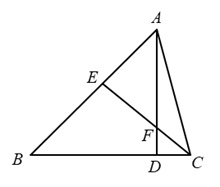
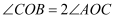 ,
, 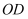 平分
平分  ,且
,且  .
. 
-
(1)
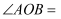
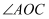 ;
;
-
(2)

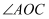 ;
;
-
(3) 求
 的度数.
的度数.
例:在数轴上表示数a和﹣2的两点之间的距离是3,求a的值.
解:如图,当数a表示的点在﹣2表示的数的左边时,a=﹣2﹣3=﹣5
当数a表示的点在﹣2表示的数的右边时,a=﹣2+3=1
所以,a=﹣5或1
请你仿照以上例题的方法,解决下列问题(写出必要的解题过程)
-
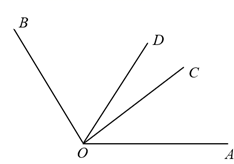
(1) 同一平面内已知∠AOB=70°,∠BOC=15°,求∠AOC的度数.
-
(2) 已知ab>0,求
 +
+ 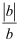 的值.
的值.
-
(3) 小明去商店购买笔记本,某笔记本的标价为每本2.5元,商店搞促销:购买该笔记本10本以下(包括10本)按原价出售,购买10本以上,从第11本开始按标价的50%出售.
①若小明购买x本笔记本,需付款多少元?
②若小明两次购买该笔记本,第二次买的本数是第一次的两倍,费用却只是第一次的1.8倍,这种情况存在吗?如果存在,请求出两次购买的笔记本数;如果不存在,请说明理由.
 .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
-
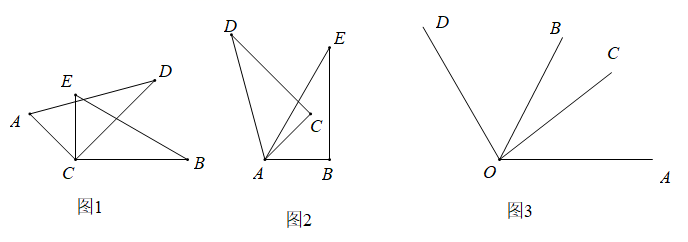
(1) 如图1,将一副直角三角尺的直角顶点C叠放在一起,经探究发现∠ACB与∠DCE的和不变.证明过程如下:
由题可知∠BCE=∠ACD=90°
∴∠ACB= +∠BCD.
∴∠ACB=90°+∠BCD.
∴∠ACB+∠DCE
=90°+∠BCD+∠DCE
=90°+∠BCE
∵∠BCE=90°,
∴∠ACB+∠DCE=.
-
(2) 如图2,若将两个含有60°的三角尺叠放在一起,使60°锐角的顶点A重合,则∠DAB与∠CAE有怎样的数量关系,并说明理由;
-
(3) 如图3,已知∠AOB=α,∠COD=β(α,β都是锐角),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的数量关系.
给出规定:如果P,Q两点的距离有最小值,那么我们称这个最小值为图形M—N的亲和距离;记作:d(图形M,图形N).特别地,当P,Q两点重合时,d(图形M,图形N)=0
举例说明:如图,数轴上的点A表示的数是1,点B,C表示的数分别是2与3,那么d(点A,线段BC)=1
根据以上定义完成下列问题:数轴上的点D,点E表示的数分别是x,x+1,点O为原点,
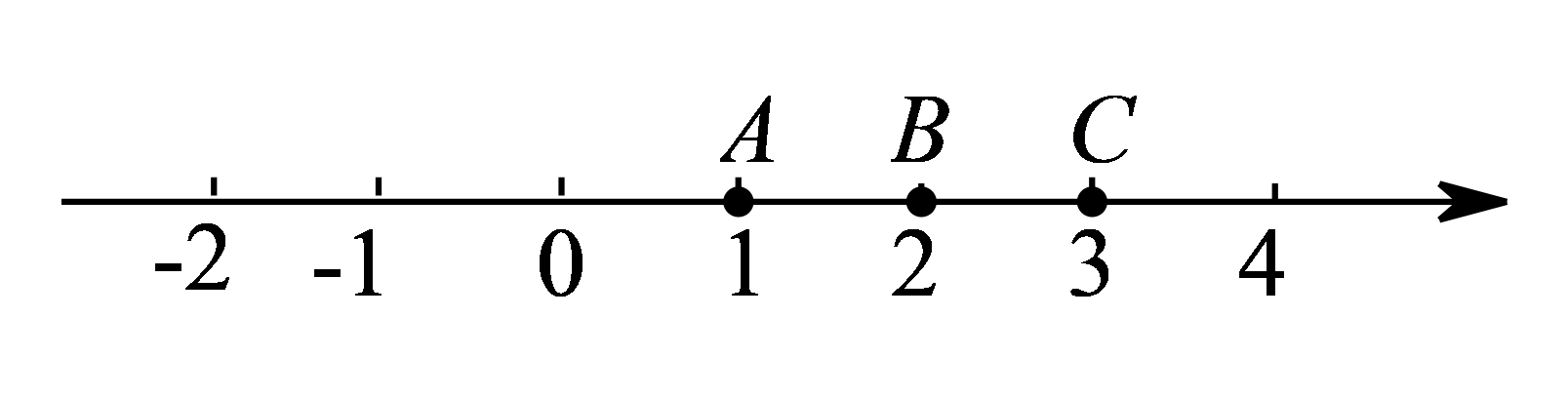
-
(1) 当x=1时,d(原点O,线段DE)=;
-
(2) 如果d(原点O,线段DE)=3,那么
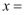 ;
;
-
(3) 数轴上的点F,点G表示的数分别是y,y+4,如果d(线段DE,线段FG)=2,直接写出
 的值.
的值.
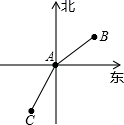
 点出发沿北偏东
点出发沿北偏东  方向行进至点
方向行进至点  ,乙从
,乙从  点出发沿南偏西
点出发沿南偏西 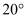 方向行进至点
方向行进至点  ,则
,则 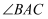 等于( )
等于( )
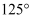 B .
B . 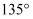 C .
C .  D .
D .