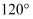дёүи§’еҪўзҡ„еҶ…еҲҮеңҶдёҺеҶ…еҝғ зҹҘиҜҶзӮ№йўҳеә“

еҰӮеӣҫпјҢеңЁв–іABCдёӯпјҢвҲ A=70В°пјҺвҠҷOжҲӘв–іABCзҡ„дёүжқЎиҫ№жүҖеҫ—зҡ„ејҰй•ҝзӣёзӯүпјҢеҲҷвҲ BOCзҡ„еәҰж•°дёәпјҲгҖҖгҖҖпјү

еҰӮеӣҫзӮ№IжҳҜв–іABCзҡ„еҶ…еҝғпјҢвҲ BIC=130В°пјҢеҲҷвҲ BAC=пјҲгҖҖгҖҖпјү

еҸӨеёҢи…Ҡзҡ„еҮ дҪ•еӯҰ家жө·дјҰи§ЈеҶідәҶиҝҷдёӘй—®йўҳпјҢеңЁд»–зҡ„и‘—дҪңгҖҠеәҰйҮҸи®әгҖӢдёҖд№Ұдёӯз»ҷеҮәдәҶи®Ўз®—е…¬ејҸп№Јп№Јжө·дјҰе…¬ејҸS= 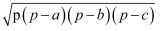 пјҲе…¶дёӯaпјҢbпјҢcжҳҜдёүи§’еҪўзҡ„дёүиҫ№й•ҝпјҢp=
пјҲе…¶дёӯaпјҢbпјҢcжҳҜдёүи§’еҪўзҡ„дёүиҫ№й•ҝпјҢp= 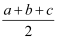 пјҢSдёәдёүи§’еҪўзҡ„йқўз§ҜпјүпјҢ并з»ҷеҮәдәҶиҜҒжҳҺ
пјҢSдёәдёүи§’еҪўзҡ„йқўз§ҜпјүпјҢ并з»ҷеҮәдәҶиҜҒжҳҺ
дҫӢеҰӮпјҡеңЁв–іABCдёӯпјҢa=3пјҢb=4пјҢc=5пјҢйӮЈд№Ҳе®ғзҡ„йқўз§ҜеҸҜд»Ҙиҝҷж ·и®Ўз®—пјҡ
вҲөa=3пјҢb=4пјҢc=5
вҲҙp= 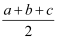 =6
=6
вҲҙS= 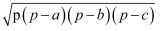 =
=  =6
=6
дәӢе®һдёҠпјҢеҜ№дәҺе·ІзҹҘдёүи§’еҪўзҡ„дёүиҫ№й•ҝжұӮдёүи§’еҪўйқўз§Ҝзҡ„й—®йўҳпјҢиҝҳеҸҜз”ЁжҲ‘еӣҪеҚ—е®Ӣж—¶жңҹж•°еӯҰ家з§Ұд№қйҹ¶жҸҗеҮәзҡ„з§Ұд№қйҹ¶е…¬ејҸзӯүж–№жі•и§ЈеҶіпјҺ
еҰӮеӣҫпјҢеңЁв–іABCдёӯпјҢBC=5пјҢAC=6пјҢAB=9
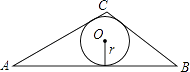
-
пјҲ1пјү з”Ёжө·дјҰе…¬ејҸжұӮв–іABCзҡ„йқўз§Ҝпјӣ
-
пјҲ2пјү жұӮв–іABCзҡ„еҶ…еҲҮеңҶеҚҠеҫ„rпјҺ

 п№Ј3
C . BC+AB=2
п№Ј3
C . BC+AB=2  +4
D . BCп№ЈAB=2
+4
D . BCп№ЈAB=2
 зҡ„дёӨдёӘж №пјҢеҲҷиҜҘзӣҙи§’дёүи§’еҪўзҡ„еҶ…еҲҮеңҶзҡ„еҚҠеҫ„r =пјҺ
зҡ„дёӨдёӘж №пјҢеҲҷиҜҘзӣҙи§’дёүи§’еҪўзҡ„еҶ…еҲҮеңҶзҡ„еҚҠеҫ„r =пјҺ

 дёәжӯЈдёүи§’еҪў
дёәжӯЈдёүи§’еҪў  зҡ„еҶ…еҲҮеңҶпјҢ
зҡ„еҶ…еҲҮеңҶпјҢ  дёәеҲҮзӮ№пјҢеӣӣиҫ№еҪў
дёәеҲҮзӮ№пјҢеӣӣиҫ№еҪў  жҳҜвҠҷ
жҳҜвҠҷ  зҡ„еҶ…жҺҘжӯЈж–№еҪўпјҢ
зҡ„еҶ…жҺҘжӯЈж–№еҪўпјҢ  пјҢеҲҷжӯЈдёүи§’еҪў
пјҢеҲҷжӯЈдёүи§’еҪў  зҡ„иҫ№й•ҝдёә( )
зҡ„иҫ№й•ҝдёә( )
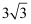 C .
C . 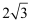 D .
D . 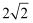

 дёҺxиҪҙдәӨдәҺAгҖҒBдёӨзӮ№пјҢдёҺyиҪҙдәӨдәҺCзӮ№пјҢиҝһжҺҘ
дёҺxиҪҙдәӨдәҺAгҖҒBдёӨзӮ№пјҢдёҺyиҪҙдәӨдәҺCзӮ№пјҢиҝһжҺҘ  гҖҒ
гҖҒ  пјҢе·ІзҹҘзӮ№AгҖҒCзҡ„еқҗж Үдёә
пјҢе·ІзҹҘзӮ№AгҖҒCзҡ„еқҗж Үдёә  гҖҒ
гҖҒ  пјҺ
пјҺ 
-
пјҲ1пјү жұӮжҠӣзү©зәҝзҡ„иЎЁиҫҫејҸпјӣ
-
пјҲ2пјү зӮ№PжҳҜзәҝж®ө
 дёӢж–№жҠӣзү©зәҝдёҠзҡ„дёҖеҠЁзӮ№пјҢеҰӮжһңеңЁxиҪҙдёҠеӯҳеңЁзӮ№QпјҢдҪҝеҫ—д»ҘзӮ№BгҖҒCгҖҒPгҖҒQдёәйЎ¶зӮ№зҡ„еӣӣиҫ№еҪўдёәе№іиЎҢеӣӣиҫ№еҪўпјҢжұӮзӮ№Qзҡ„еқҗж Үпјӣ
дёӢж–№жҠӣзү©зәҝдёҠзҡ„дёҖеҠЁзӮ№пјҢеҰӮжһңеңЁxиҪҙдёҠеӯҳеңЁзӮ№QпјҢдҪҝеҫ—д»ҘзӮ№BгҖҒCгҖҒPгҖҒQдёәйЎ¶зӮ№зҡ„еӣӣиҫ№еҪўдёәе№іиЎҢеӣӣиҫ№еҪўпјҢжұӮзӮ№Qзҡ„еқҗж Үпјӣ
-
пјҲ3пјү еҰӮеӣҫ2пјҢиӢҘзӮ№MжҳҜ
 еҶ…дёҖеҠЁзӮ№пјҢдё”ж»Ўи¶і
еҶ…дёҖеҠЁзӮ№пјҢдё”ж»Ўи¶і  пјҢиҝҮзӮ№MдҪң
пјҢиҝҮзӮ№MдҪң  пјҢеһӮи¶ідёәNпјҢи®ҫ
пјҢеһӮи¶ідёәNпјҢи®ҫ 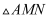 зҡ„еҶ…еҝғдёәIпјҢиҜ•жұӮ
зҡ„еҶ…еҝғдёәIпјҢиҜ•жұӮ  зҡ„жңҖе°ҸеҖјпјҺ
зҡ„жңҖе°ҸеҖјпјҺ

-
пјҲ1пјү еҰӮеӣҫ1пјҢеңЁзӯүйӮ»иҫ№дә’иЎҘеӣӣиҫ№еҪўABCDдёӯпјҢAD=CDпјҢдё”AD//BCпјҢ BC=2ADпјҢжұӮвҲ Bзҡ„еәҰж•°;
-
пјҲ2пјү еҰӮеӣҫ2пјҢеӣӣиҫ№еҪўABCDеҶ…жҺҘдәҺеңҶOпјҢиҝһз»“DOдәӨACдәҺзӮ№E (дёҚдёҺзӮ№OйҮҚеҗҲ)пјҢиӢҘEжҳҜACзҡ„дёӯзӮ№пјҢжұӮиҜҒ:еӣӣиҫ№еҪўABCDжҳҜзӯүйӮ»иҫ№дә’иЎҘеӣӣиҫ№еҪў;
-
пјҲ3пјү еңЁ(2) зҡ„жқЎд»¶дёӢпјҢ延й•ҝDOдәӨBCдәҺзӮ№FпјҢдәӨеңҶ0дәҺзӮ№GпјҢиӢҘеј§BG=еј§AB, tanвҲ ABC=
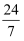 пјҢAC=12,жұӮFGзҡ„й•ҝ;
пјҢAC=12,жұӮFGзҡ„й•ҝ;
-
пјҲ4пјү еҰӮеӣҫ3,еӣӣиҫ№еҪўABCDеҶ…жҺҘдәҺеңҶOпјҢAB=BC, BDдёәеңҶ0зҡ„зӣҙеҫ„пјҢиҝһз»“AO并延й•ҝдәӨBCдәҺзӮ№EпјҢдәӨеңҶ0дәҺзӮ№F,иҝһз»“FCпјҢи®ҫtanвҲ BAF=xпјҢ
 пјҢжұӮyдёҺxд№Ӣй—ҙзҡ„еҮҪж•°е…ізі»ејҸ.
пјҢжұӮyдёҺxд№Ӣй—ҙзҡ„еҮҪж•°е…ізі»ејҸ.
 пјҢж»Ўи¶і
пјҢж»Ўи¶і 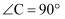 пјҢ
пјҢ  пјҢ
пјҢ 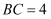 пјҢ
пјҢ 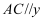 иҪҙпјҢеҪ“зӮ№
иҪҙпјҢеҪ“зӮ№  пјҢзӮ№
пјҢзӮ№  еҸҠ
еҸҠ 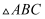 зҡ„еҶ…еҝғ
зҡ„еҶ…еҝғ  еңЁеҗҢдёҖеҸҚжҜ”дҫӢеҮҪж•°
еңЁеҗҢдёҖеҸҚжҜ”дҫӢеҮҪж•° 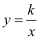 зҡ„еӣҫиұЎдёҠж—¶пјҢеҲҷ
зҡ„еӣҫиұЎдёҠж—¶пјҢеҲҷ 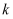 зҡ„еҖјжҳҜ.
зҡ„еҖјжҳҜ. 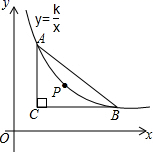

 B .
B .  C .
C .  D .
D . 
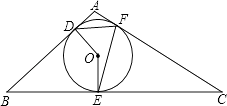
 жҳҜ
жҳҜ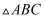 зҡ„еҶ…еҝғпјҢ
зҡ„еҶ…еҝғпјҢ зҡ„延й•ҝзәҝе’Ң
зҡ„延й•ҝзәҝе’Ң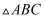 зҡ„еӨ–жҺҘеңҶзӣёдәӨдәҺзӮ№
зҡ„еӨ–жҺҘеңҶзӣёдәӨдәҺзӮ№ пјҢ иҝһжҺҘ
пјҢ иҝһжҺҘ пјҢ
пјҢ  пјҢ
пјҢ 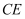 пјҢ иӢҘ
пјҢ иӢҘ пјҢ еҲҷ
пјҢ еҲҷ зҡ„еӨ§е°ҸдёәпјҲ пјү
зҡ„еӨ§е°ҸдёәпјҲ пјү
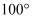 B .
B .  C .
C .  D .
D .