集合的表示法 知识点题库
由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集Q划分为两个非空的子集M与N,且满足M∪N=Q,M∩N=∅,M中的每一个元素都小于N中的每一个元素,则称(M,N)为戴德金分割试判断,对于任一戴德金分割(M,N),下列选项中,不可能成 立的是( )
A . M没有最大元素,N有一个最小元素
B . M没有最大元素,N也没有最小元素
C . M有一个最大元素,N有一个最小元素
D . M有一个最大元素,N没有最小元素
已知集合A={x|mx2+2x﹣1=0},若集合A中只有一个元素,则实数m的值为
已知集合A={x∈R|ax2+2x+1=0,a∈R}中只有一个元素,求a的值并求出这个元素.
方程组  的解集为( )
的解集为( )
 的解集为( )
的解集为( )
A . {x=2,y=1}
B .  C . {2,1}
D . {(2,1)}
C . {2,1}
D . {(2,1)}
 C . {2,1}
D . {(2,1)}
C . {2,1}
D . {(2,1)}
已知集合A={0,1,2,3,4,5},B=﹛5,6﹜,C=﹛(x,y)|x∈A,y∈A,x+y∈B﹜,则C中所含元素的个数为( )
A . 5
B . 6
C . 11
D . 12
解答题。
-
(1) 已知集合A={x|ax2﹣3x+1=0,a∈R},若A中只有一个元素,求a的取值范围.
-
(2) 集合A={x|x2﹣6x+5<0},C={x|3a﹣2<x<4a﹣3},若C⊆A,求a的取值范围.
已知集合M={a|  ∈N+ , 且a∈Z},则M等于( )
∈N+ , 且a∈Z},则M等于( )
 ∈N+ , 且a∈Z},则M等于( )
∈N+ , 且a∈Z},则M等于( )
A . {2,3}
B . {1,2,3,4}
C . {1,2,3,6}
D . {﹣1,2,3,4}
用C(A)表示非空集合A中的元素个数.已知A={1,2},B={x|(x2+ax)•(x2+ax+2)=0,若|C(A)﹣C(B)|=1,设实数a的所有可能取值集合是S,则C(S)=( )
A . 4
B . 3
C . 2
D . 1
用列举法表示集合{(x,y)|2x+y﹣5=0,x∈N,y∈N}=.
方程x2﹣5x+6=0的解集可表示为,方程组  的解集可表示为.
的解集可表示为.
 的解集可表示为.
的解集可表示为.
设A是由有限个正整数组成的集合,若存在两个集合B,C满足:①B∩C=∅;②B∪C=A;③B的元素之和等于C的元素之和,则称集合A“可均分”.
-
(1) 证明:集合A={1,2,3,4,5,6,7,8}“可均分”;
-
(2) 证明:集合A={2015+1,2015+2,…,2015+93}“可均分”;
-
(3) 求出所有的正整数k,使得A={2015+1,2015+2,…,2015+k}“可均分”.
已知λ,μ为常数,且为正整数,λ为质数且大于2,无穷数列{an}的各项均为正整数,其前n项和为Sn , 对任意正整数n,2Sn=λan﹣μ,数列{an}中任意两不同项的和构成集合A.
-
(1) 证明无穷数列{an}为等比数列,并求λ的值;
-
(2) 如果2010∈A,求μ的值;
-
(3) 当n≥1,设集合
 中元素的个数记为bn , 求bn .
中元素的个数记为bn , 求bn .
用列举法表示下列给定的集合:
-
(1) 大于
 且小于5的整数组成的集合A;
且小于5的整数组成的集合A;
-
(2) 方程x2−9=0的实数根组成的集合B;
-
(3) 小于8的质数组成的集合C.
用列举法表示集合  .
.
 .
.
把集合  用列举法表示.
用列举法表示.
 用列举法表示.
用列举法表示.
方程组 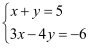 的解集是( )
的解集是( )
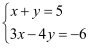 的解集是( )
的解集是( )
A . 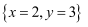 B .
B . 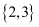 C .
C . 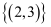 D .
D . 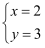
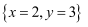 B .
B . 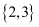 C .
C . 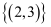 D .
D . 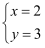
用列举法表示集合 

10的所有正因数组成的集合用列举法表示为.
下列命题为真命题的是( )
A . 集合  有两个子集
B . 若
有两个子集
B . 若 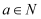 ,则
,则 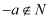 C . 集合
C . 集合  里面有6个元素
D . 平面直角坐标系中第二、四象限的点的集合可以表示为
里面有6个元素
D . 平面直角坐标系中第二、四象限的点的集合可以表示为 
 有两个子集
B . 若
有两个子集
B . 若 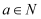 ,则
,则 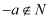 C . 集合
C . 集合  里面有6个元素
D . 平面直角坐标系中第二、四象限的点的集合可以表示为
里面有6个元素
D . 平面直角坐标系中第二、四象限的点的集合可以表示为 
已知集合  ,则M中元素的个数为( )
,则M中元素的个数为( )
 ,则M中元素的个数为( )
,则M中元素的个数为( )
A . 1
B . 2
C . 3
D . 0
最近更新



