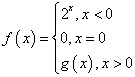ж№–еҚ—зңҒй•ҝжІҷеёӮ2017_2018еӯҰе№ҙй«ҳдёҖж•°еӯҰдёҠеӯҰжңҹ第дёҖж¬ЎжЁЎеқ—жЈҖжөӢиҜ•йўҳиҜ•еҚ·еҸҠзӯ”жЎҲ
| 1. | иҜҰз»ҶдҝЎжҒҜ |
|
еҰӮжһң В A.
|
|
| 2. | иҜҰз»ҶдҝЎжҒҜ |
|
дёҚи®ә В A.В В
|
|
| 3. | иҜҰз»ҶдҝЎжҒҜ |
|
еҮҪж•° В A. C.
|
|
| 4. | иҜҰз»ҶдҝЎжҒҜ |
|
еҮҪж•° В A.
|
|
| 5. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫеҮҪж•° В A.
|
|
| 6. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫйӣҶеҗҲ В A.
|
|
| 7. | иҜҰз»ҶдҝЎжҒҜ |
|
В A.
|
|
| 8. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫеҮҪж•° В A.В
|
|
| 9. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘе®һж•° В A.
|
|
| 10. | иҜҰз»ҶдҝЎжҒҜ |
|
.и®Ўз®— В A.
|
|
| 11. | иҜҰз»ҶдҝЎжҒҜ |
|
.еҰӮжһң
|
|
| 12. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘеҒ¶еҮҪж•°
|
|
| 13. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫе®ҡд№үеңЁRдёҠзҡ„еҮҪж•°
|
|
| 14. | иҜҰз»ҶдҝЎжҒҜ |
|
и®ҫ
|
|
| 15. | иҜҰз»ҶдҝЎжҒҜ |
|
В еҜ№дәҺеҮҪж•°
|
|
| 16. | иҜҰз»ҶдҝЎжҒҜ |
|
В В е·ІзҹҘйӣҶеҗҲ В В пјҲ1пјүжұӮйӣҶеҗҲ В В пјҲ2пјүиӢҘ
|
|
| 17. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘ В В пјҲ1пјү В В пјҲ2пјү
|
|
| 18. | иҜҰз»ҶдҝЎжҒҜ |
|
еҰӮеӣҫпјҢзҹ©еҪў В В пјҲ1пјүеҶҷеҮәзҹ©еҪў В В пјҲ2пјүй—®
|
|
| 19. | иҜҰз»ҶдҝЎжҒҜ |
|
В В В е·ІзҹҘеҮҪж•° В В пјҲ1пјүжұӮ В В пјҲ2пјүи®ҫ
|
|
| 20. | иҜҰз»ҶдҝЎжҒҜ |
|
е·ІзҹҘжҹҗдә§е“Ғе…ізЁҺдёҺеёӮеңәдҫӣеә”йҮҸ В В пјҲ1пјүж №жҚ®еӣҫиұЎжұӮ В В пјҲ2пјүиӢҘеёӮеңәйңҖжұӮйҮҸдёә
|
|
- й«ҳдёҖдёӢеҶҢжңҹжң«ж•°еӯҰйўҳе…Қиҙ№еңЁзәҝжЈҖжөӢпјҲ2019-2020е№ҙжұҹиӢҸзңҒе®ҝиҝҒеёӮпјү
- 2019-2020е№ҙй«ҳдёүдёҠеҶҢ12жңҲжңҲиҖғж•°еӯҰиҖғйўҳпјҲжІіеҢ—зңҒиЎЎж°ҙеёӮж·ұе·һеёӮй•ҝжұҹдёӯеӯҰпјү
- й«ҳдәҢдёӢеҶҢжңҹжң«ж•°еӯҰж— зәёиҜ•еҚ·е®Ңж•ҙзүҲпјҲ2019-2020е№ҙжұҹиӢҸзңҒж·®е®үеёӮпјү
- еӨ§еәҶеёӮй«ҳдәҢж•°еӯҰдёҠеҶҢжңҹжң«иҖғиҜ•ж‘ёеә•иҖғиҜ•йўҳ
- жӯҰеЁҒеёӮй«ҳдәҢж•°еӯҰжңҲиҖғжөӢйӘҢпјҲ2019е№ҙдёӢеҚҠжңҹпјүе…Қиҙ№жЈҖжөӢиҜ•еҚ·
- жөҷжұҹзңҒеҸ°е·һеёӮ第дёҖдёӯеӯҰ2020-2021е№ҙй«ҳдёүдёҠжңҹжңҹдёӯж•°еӯҰеңЁзәҝиҖғиҜ•йўҳе…Қиҙ№з»ғд№
- е®үеҫҪ2020е№ҙй«ҳдёүж•°еӯҰдёӢеҶҢеёҰеҸӮиҖғзӯ”жЎҲдёҺи§Јжһҗ
- дёҠжө·еёӮй«ҳдәҢж•°еӯҰдёҠеҶҢжңҲиҖғиҜ•еҚ·еңЁзәҝжөӢйӘҢе®Ңж•ҙзүҲ