勾股定理的证明 知识点题库
如图,梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图所示。
(1)请你运用两种方法计算梯形ABCD的面积;
(2)根据(1)的计算,探索a,b,c三者之间的关系,并用式子表示出来。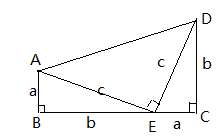
2002年8月在北京召开的国际数学家大会会标,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为13,小正方形的面积是1 , 直角三角形较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
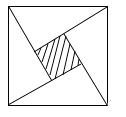
A . 13
B . 19
C . 25
D . 169
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积分别是为1、13,则直角三角形两直角边和a+b=
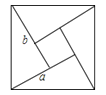
[问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法.我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数学关系”(勾股定理)带到其它星球,作为地球人与其他星球“人”进行第一次“谈话”的语言;
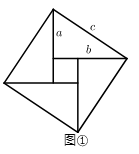
[定理表述]请你根据图1中的直角三角形叙述勾股定理;
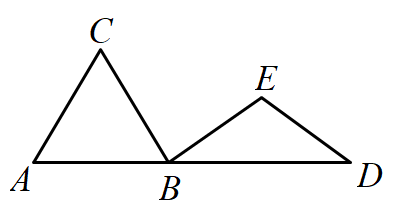
[尝试证明]以图1中的直角三角形为基础,将两个直角边长为a,b,斜边长为c的三角形按如图所示的方式放置,连接两个之间三角形的另外一对锐角的顶点(如图2),请你利用图2,验证勾股定理;
[知识扩展]利用图2中的直角梯形,我们可以证明 <
<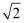 , 其证明步骤如下:
, 其证明步骤如下:
∵BC=a+b,AD=,
又∵在直角梯形ABCD中,有BCAD(填大小关系),即 ,
∴ <
<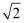 .
.
如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )

A . 8
B . 6
C . 4
D . 5
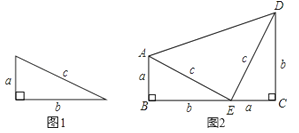
意大利著名画家达•芬奇验证勾股定理的方法如下:
①在一张长方形的纸板上画两个边长分别为a、b的正方形,并连接BC、FE.
②沿ABCDEF剪下,得两个大小相同的纸板Ⅰ、Ⅱ,请动手做一做.
③将纸板Ⅱ翻转后与Ⅰ拼成其他的图形.
④比较两个多边形ABCDEF和A′B′C′D′E′F′的面积,你能验证勾股定理吗?
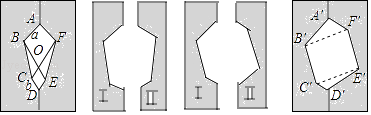
(以面积找规律)如图,由两个边长分别为a、b、c的直角三角形和一个两直角边都是c的直角三角形拼成一个新图形,使用不同的方法计算这个图形的面积,你发现了什么?
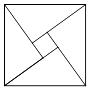
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若正方形EFGH的边长为2,则S1+S2+S3=.
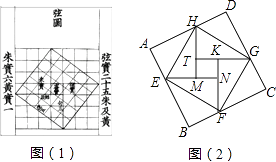
2002年8月,在北京召开国际数学家大会,大会的会标取材于我国古代数学家赵爽的《勾股圆方图》.其中的“弦图”是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,如图所示.如果直角三角形的直角边分别为a,b(a>b),斜边为c,那么小正方形的面积可以表示为.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是49,小正方形的面积为4,直角三角形的两直角边长分别为a,b,那么下列结论:
(1)a2+b2=49,(2)b﹣a=2,(3)ab=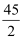 , (4)a+b=
, (4)a+b= 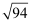 中,
中,
(1)a2+b2=49,(2)b﹣a=2,(3)ab=
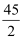 , (4)a+b=
, (4)a+b= 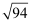 中,
中,正确结论的个数有( )

A . 4个
B . 3个
C . 2个
D . 1个
我国三国时期数学家赵爽为了证明勾股定理,创造了一副“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形 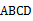 的边长为14,正方形
的边长为14,正方形 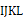 的边长为2,且
的边长为2,且  ,则正方形
,则正方形  的边长为.
的边长为.

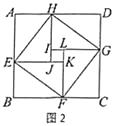
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2  EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )
 EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( ) 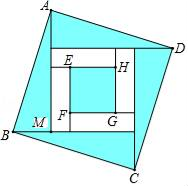
A . 14S
B . 13S
C . 12S
D . 11S
如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为  和
和 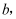 斜边长为
斜边长为 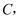 图(2)是以
图(2)是以  为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
 和
和 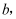 斜边长为
斜边长为 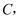 图(2)是以
图(2)是以  为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形. 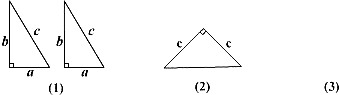
-
(1) 在图(3)处画出拼成的这个图形的示意图;
-
(2) 利用(1)画出的图形证明勾股定理.
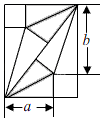
我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若a=2,b=3,则该矩形的面积为.
如图所示,在正方形  中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为
中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为  的正方形,则下列等式成立的是( )
的正方形,则下列等式成立的是( )
 中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为
中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为  的正方形,则下列等式成立的是( )
的正方形,则下列等式成立的是( ) 
A . 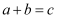 B .
B . 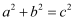 C .
C . 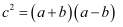 D .
D . 
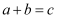 B .
B . 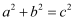 C .
C . 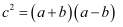 D .
D . 
如图
-
(1) 阅读理解:我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;
-
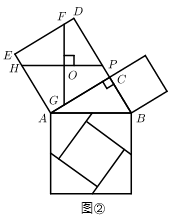
(2) 问题解决:勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形
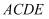 的中心
的中心  ,作
,作  ,将它分成4份.所分成的四部分和以
,将它分成4份.所分成的四部分和以  为边的正方形恰好能拼成以
为边的正方形恰好能拼成以  为边的正方形.若
为边的正方形.若 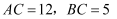 ,求
,求 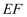 的值;
的值;
-
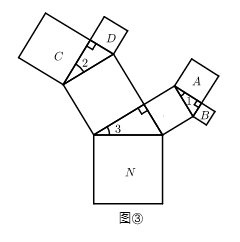
(3) 拓展探究:如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形
 的边长为定值
的边长为定值  ,小正方形
,小正方形 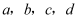 的边长分别为
的边长分别为 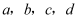 .已知
.已知 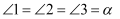 ,当角
,当角 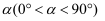 变化时,探究
变化时,探究  与
与  的关系式,并写出该关系式及解答过程(
的关系式,并写出该关系式及解答过程(  与
与  的关系式用含
的关系式用含  的式子表示).
的式子表示).
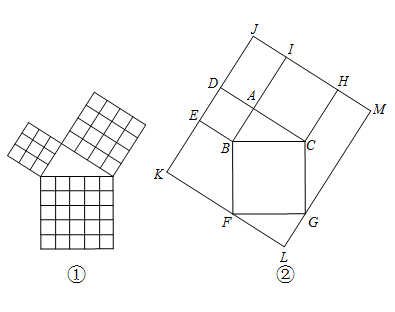
勾股定理是几何中的一个重要定理。在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载。如图①所示是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理。如图②所示是由图①放人长方形KLMJ内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为( )
A . 90
B . 100
C . 110
D . 121
如图,小明用4个图1中的矩形组成图2,其中四边形ABCD,EFGH,MNPQ都是正方形,证明: . (提示;运用面积等量关系)
. (提示;运用面积等量关系)
 . (提示;运用面积等量关系)
. (提示;运用面积等量关系)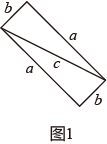
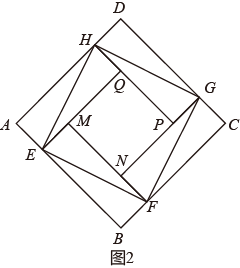
如图,AC=BC=BE=DE=10cm,点A、B、D在同一条直线上,AB=12cm,BD=16cm,则点C和点E之间的距离是( )
A . 6cm
B . 7cm
C . 8cm
D . 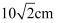
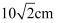
下面图形能够验证勾股定理的有( )个
A . 4个
B . 3个
C . 2个
D . 1个
最近更新



