勾股定理的证明 知识点题库


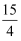 C . 5
D .
C . 5
D . 

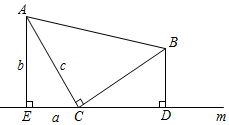
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b﹣A.
∵S四边形ADCB=S△ACD+S△ABC=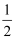 b2+
b2+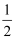 ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=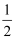 c2+
c2+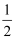 a(b﹣a)
a(b﹣a)
∴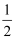 b2+
b2+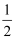 ab=
ab=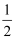 c2+
c2+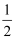 a(b﹣a)
a(b﹣a)
∴a2+b2=c2
解决问题:请参照上述证法,利用图2完成下面的证明:将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .


 EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( ) 

 、
、 
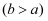 ,斜边为
,斜边为  .我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,
.我国古代数学家赵爽用四个这样的直角三角形拼成了如图的正方形,
-
(1) 探究活动:如图1,中间围成的小正方形的边长为(用含有
 、
、  的代数式表示);
的代数式表示);
-
(2) 探究活动:如图1,用不同的方法表示这个大正方形的面积,并写出你发现的结论;
-
(3) 新知运用:根据你所发现的结论完成下列问题
①某个直角三角形的两条直角边
 、
、  满足式子
满足式子  ,求它的斜边
,求它的斜边  的值;
的值;②由①中结论,求此三角形斜边
 上的高。
上的高。③如图2,这个勾股树图形是由正方形和直角三角形组成的,若正方形
 、
、  、
、  、
、  的面积分别为
的面积分别为 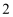 ,4,
,4,  ,
, 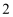 .求最大的正方形
.求最大的正方形  的边长。
的边长。
【材料】如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理: 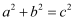 .
.


【请回答】如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?
-
(1) 【理解】
如图,两个边长分别为
 、
、  、
、  的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是  的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;
的直角三角形拼成一个梯形.用两种不同的方法计算梯形的面积,并写出你发现的结论;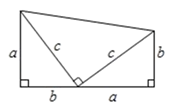
-
(2) 如图2,
 行
行  列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:
列的棋子排成一个正方形,用两种不同的方法计算棋子的个数,可得等式:  ;
; 
-
(3) 【运用】
 边形有
边形有  个顶点,在它的内部再画
个顶点,在它的内部再画  个点,以(
个点,以( 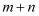 )个点为顶点,把
)个点为顶点,把  边形剪成若干个三角形,设最多可以剪得
边形剪成若干个三角形,设最多可以剪得 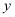 个这样的三角形.当
个这样的三角形.当 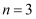 ,
, 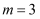 时,如图,最多可以剪得
时,如图,最多可以剪得 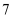 个这样的三角形,所以
个这样的三角形,所以 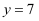 .
.
①当
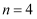 ,
, 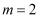 时,如图,
时,如图, 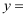 ;当
;当 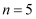 ,
,  时,
时,  ;
;
②对于一般的情形,在
 边形内画
边形内画  个点,通过归纳猜想,可得
个点,通过归纳猜想,可得 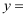 (用含
(用含  、
、  的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.
的代数式表示).请对同一个量用算两次的方法说明你的猜想成立.

 ,饶其锐角顶点逆时针旋转90°得
,饶其锐角顶点逆时针旋转90°得  ,所以
,所以  ,且四边形
,且四边形 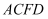 是一个正方形,它的面积和四边形
是一个正方形,它的面积和四边形  面积相等,而四边形
面积相等,而四边形  面积等于
面积等于  和
和  的面积之和,根据图形写出一种证明勾股定理的方法.
的面积之和,根据图形写出一种证明勾股定理的方法. 
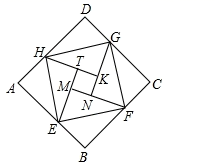
-
(1) 求证:
 ;
;
-
(2) 若设△AEC三边分别为a、b、c,利用此图证明勾股定理.



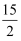 C .
C . 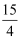 D . 3
D . 3
 、
、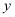 的长方形和中间一个小正方形组成的大正方形.
的长方形和中间一个小正方形组成的大正方形.
-
(1) 若大正方形的面积为36,小正方形的面积为4,则
 值为;则
值为;则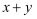 的值为;
的值为;
-
(2) 若小长方形两边长为
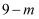 和
和 , 则大正方形的边长为;
, 则大正方形的边长为;若满足
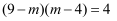 , 则
, 则 的值为;
的值为; -
(3) 如图2,正方形
 的边长是
的边长是 , 它由四个直角边长分别是
, 它由四个直角边长分别是 ,
,  的直角三角形和中间一个小正方形组成的,猜想
的直角三角形和中间一个小正方形组成的,猜想 ,
,  ,
,  三边的数量关系,并说明理由.
三边的数量关系,并说明理由.

小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x=
-
(1) 小亮也发现了另一种求正方形边长的方法:
利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程:
-
(2) 请结合小明和小亮得到的结论验证勾股定理.
-
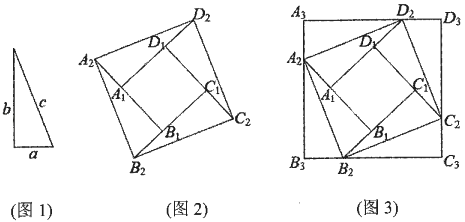
(1) 正方形A1B1C1D1的边长为.
-
(2) 请你用两种不同的方法表示正方形A2B2C2D2面积,并写出a2 , b2 , c2之间的数量关系.
-
(3) 若将剩余的四张纸片按图3的方式拼在图2外围,可得正方形A3B3C3D3 . 若正方形A1B1C1D1的面积为49,正方形A3B3C3D3的面积为289,求正方形A2B2C2D2的面积.



