勾股定理的证明 知识点题库
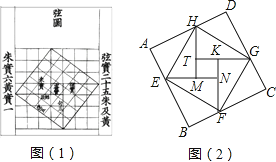
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3 . 若正方形EFGH的边长为2,则S1+S2+S3= .

 D . 4+2
D . 4+2

①a2+b2=13;②b2=1;③a2﹣b2=12;④ab=6.
其中正确结论序号是 .

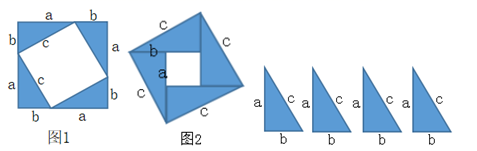
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=  b2+
b2+  ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=  c2+
c2+  a(b﹣a)
a(b﹣a)
∴  b2+
b2+  ab=
ab=  c2+
c2+  a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .


-
(1) 画出拼成的这个图形的示意图,并用它验证勾股定理;
-
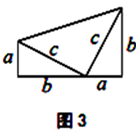
(2) 假设图3中的直角三角形有若干个,你能运用图中所给的直角三角形拼出另一种能够验证勾股定理的图形吗?画出拼成图形的示意图(不写验证过程).


-
(1) 求证:DE⊥AB;
-
(2) 若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD=
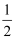 c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形.直角三角形的两条直角边长分别为a、b ,斜边长为c.

-
(1) 图中阴影部分的面积用两种方法可分别表示为、;
-
(2) 你能得出的a, b, c之间的数量关系是(等号两边需化为最简形式);
-
(3) 若一直角三角形的两条直角边长为5和12, 则其斜边长为.
-
(4) 用不同的方法计算这个正方体的体积,就可以得到一个等式,这个等式可以为;
-
(5) 已知
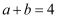 ,
, 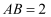 ,利用上面的规律求
,利用上面的规律求  的值.
的值.
了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2 .
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵ 
 b2+
b2+  ab.
ab.
又∵ 
 c2+
c2+  a(b-a).
a(b-a).
∴  b2+
b2+  ab=
ab=  c2+
c2+  a(b-a)
a(b-a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

股定理)”带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.

-
(1) 请你根据图(1)中的直角三角形叙述勾股定理(用文字及符号语言叙述).
-
(2) 以图(1)中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图(2))。请你利用图(2)证明勾股定理.
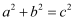 .请你写出证明过程.
.请你写出证明过程. 

-
(1) 用4个全等的Rt△拼成如图1所示的大正方形,大正方形的面积可以表示为
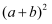 ,还可以表示为,所以
,还可以表示为,所以  ,将
,将 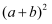 展开整理后,可进一步的得到等式:.
展开整理后,可进一步的得到等式:.
-
(2) 用4个全等的Rt△还可以拼成如图2所示的大正方形,请利用图2证明(1)中等式成立.
-
(3) 若已知Rt△中,
 ,利用你得到的等式求
,利用你得到的等式求  的值.
的值.




(背景阅读)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了验证勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(实践操作)
-
(1) 请叙述勾股定理;
-
(2) 验证勾股定理,人们已经找到了400多种方法,请从下列几种常见的验证方法中任选一种来验证该定理:(以下图形均满足验证勾股定理所需的条件)
-
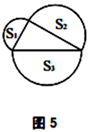
(3) (探索发现)如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足
 的有个;
的有个;
-
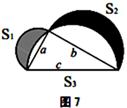
(4) 如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为
 、
、  ,直角三角形面积为
,直角三角形面积为  ,请判断
,请判断  、
、  、
、  的关系并说明理由.
的关系并说明理由.
 ,斜边长为
,斜边长为  的
的  个直角三角形,请根据图2利用割补的方法验证勾股定理.
个直角三角形,请根据图2利用割补的方法验证勾股定理. 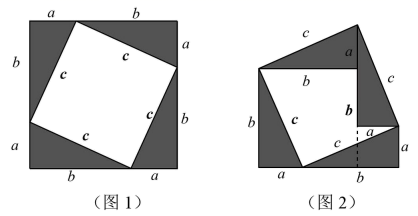

-
(1) 结合图①,求证:a2+b2=c2;
-
(2) 如图②,将这四个全等的直角三角形无缝隙无重叠地拼接在一起,得到图形ABCDEFGH,若该图形的周长为24,OH=3,求该图形的面积;
-
(3) 如图③,将八个全等的直角三角形紧密地拼接成正方形PQMN,记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S1、S2、S3。若S1+S2+S3=18,则S2=
 , 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图
, 以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图 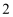 的方式放 置在最大正方形内.若图
的方式放 置在最大正方形内.若图 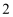 中阴影部分的面积为
中阴影部分的面积为 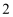 ,且
,且  ,则
,则  的长为( )
的长为( ) 
图1 图2
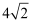 B .
B . 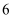 C .
C . 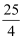 D .
D . 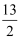
-
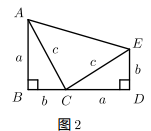
(1) 如图1是其中一条完全平方公式的几何解释,请你写出这个公式.
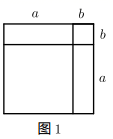
-
(2) 如图2所示,
 ,
,  ,且B,C,D在同一直线上.则
,且B,C,D在同一直线上.则 
 .
. 
-
(3) 伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的《新英格兰教育日志》上),请你写出验证过程.



