函数的最值及其几何意义 知识点题库
已知函数f(x)=ax2﹣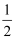 x+c(a,c∈R)满足条件f(1)=0,且对任意实数x都有f(x)≥0.
x+c(a,c∈R)满足条件f(1)=0,且对任意实数x都有f(x)≥0.
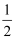 x+c(a,c∈R)满足条件f(1)=0,且对任意实数x都有f(x)≥0.
x+c(a,c∈R)满足条件f(1)=0,且对任意实数x都有f(x)≥0.(1)求a、c的值:
(2)是否存在实数m,使函数g(x)=4f(x)﹣mx在区间[m,m+2]上有最小值﹣5?若存在,请求出实数m的值;若不存在,请说明理由.
已知二次函数y=f(x),当x=2时,函数f(x)取最小值﹣1,且f(1)+f(4)=3.
(1)求f(x)的解析式;
(2)若g(x)=f(x)﹣kx在区间(1,4)上无最小值,求实数k的取值范围.
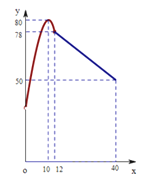
学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
设函数f(x)=|2x﹣1|
-
(1) 解关于x的不等式f(2x)≤f(x+1)
-
(2) 若实数a,b满足a+b=2,求f(a2)+f(b2)的最小值.
已知a∈R,函数f(x)=log2( 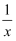 +a).
+a).
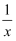 +a).
+a).
-
(1) 当a=1时,解不等式f(x)>1;
-
(2) 若关于x的方程f(x)+log2(x2)=0的解集中恰有一个元素,求a的值;
-
(3) 设a>0,若对任意t∈[
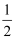 ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
已知a>0,则a+ 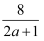 的最小值为()
的最小值为()
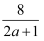 的最小值为()
的最小值为()
A . 2  B . 4
C .
B . 4
C . 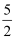 D .
D . 
 B . 4
C .
B . 4
C . 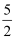 D .
D . 
已知函数f(x)=  .
.
 .
.
-
(1) 证明:∀k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
-
(2) 若∃x∈[e,e2],使得f(x)≤g(x)+
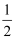 成立,求实数k的取值范围.
成立,求实数k的取值范围.
已知函数  .
.
 .
.
-
(1) 求不等式
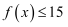 的解集;
的解集;
-
(2) 若
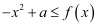 对
对 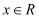 恒成立,求
恒成立,求  的取值范围.
的取值范围.
设定义域为R的奇函数y=f(x)为减函数。f(cos2θ+2msinθ)+f(-2m-2)>0恒成立,则实数m的取值范围为.
已知函数 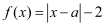 .
.
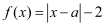 .
.
-
(1) 若
 ,解不等式
,解不等式 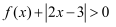 ;
;
-
(2) 关于
 的不等式
的不等式 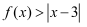 有解,求实数
有解,求实数  的取值范围.
的取值范围.
已知函数  .若不等式
.若不等式 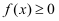 对一切
对一切 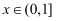 恒成立,则实数a的最小值为;若
恒成立,则实数a的最小值为;若 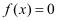 的一个根比1大,另一个根比1小,则实数a的取值范围是.
的一个根比1大,另一个根比1小,则实数a的取值范围是.
 .若不等式
.若不等式 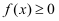 对一切
对一切 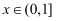 恒成立,则实数a的最小值为;若
恒成立,则实数a的最小值为;若 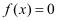 的一个根比1大,另一个根比1小,则实数a的取值范围是.
的一个根比1大,另一个根比1小,则实数a的取值范围是.
已知函数  .
.
 .
.
-
(1) 讨论函数
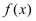 的单调区间及极值;
的单调区间及极值;
-
(2) 若关于
 的不等式
的不等式 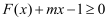 恒成立,求整数
恒成立,求整数  的最小值.
的最小值.
已知 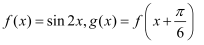 ,直线
,直线 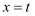 与函数
与函数 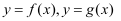 的交点分别为A , B , 则线段
的交点分别为A , B , 则线段  长度的最大值为( )
长度的最大值为( )
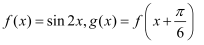 ,直线
,直线 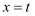 与函数
与函数 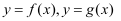 的交点分别为A , B , 则线段
的交点分别为A , B , 则线段  长度的最大值为( )
长度的最大值为( )
A . 1
B .  C .
C .  D . 2
D . 2
 C .
C .  D . 2
D . 2
已知平面单位向量 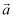 ,
, 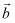 满足
满足 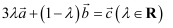 ,
, 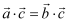 ,记
,记 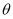 为向量
为向量  与
与 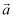 的夹角,则
的夹角,则 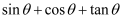 的最小值是.
的最小值是.
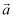 ,
, 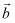 满足
满足 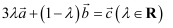 ,
, 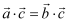 ,记
,记 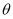 为向量
为向量  与
与 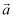 的夹角,则
的夹角,则 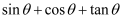 的最小值是.
的最小值是.
关于函数 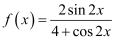 ,则下列结论中正确的有( )
,则下列结论中正确的有( )
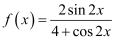 ,则下列结论中正确的有( )
,则下列结论中正确的有( ) ① 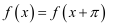 ;②
;② 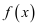 的最大值为
的最大值为 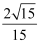 ;
;
③ 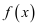 在
在 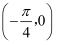 单调递增;④
单调递增;④ 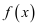 在
在 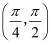 单调递减.
单调递减.
A . 1个
B . 2个
C . 3个
D . 4个
已知函数  ,若方程
,若方程 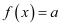 有四个不同的解
有四个不同的解  ,且
,且  ,则
,则  的最小值是,
的最小值是,  的最大值是.
的最大值是.
 ,若方程
,若方程 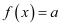 有四个不同的解
有四个不同的解  ,且
,且  ,则
,则  的最小值是,
的最小值是,  的最大值是.
的最大值是.
2022年浙江省第十七届运动会将在金华举行.主办方在建造运动会主体育场时需建造隔热层,并要求隔热层的使用年限为15年.已知每厘米厚的隔热层建造成本是4万元,设每年的能源消耗费用为  (万元),隔热层厚度为
(万元),隔热层厚度为  (厘米),两者满足关系式:
(厘米),两者满足关系式: 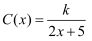 (
( 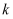 为常数,
为常数, 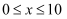 ).若无隔热层,则每年的能源消耗费用为6万元.15年的总维修费用为10万元.记
).若无隔热层,则每年的能源消耗费用为6万元.15年的总维修费用为10万元.记 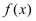 为15年的总费用.(总费用=隔热层的建造成本费用
为15年的总费用.(总费用=隔热层的建造成本费用 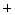 使用15年的能源消耗费用
使用15年的能源消耗费用 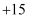 年的总维修费用).
年的总维修费用).
 (万元),隔热层厚度为
(万元),隔热层厚度为  (厘米),两者满足关系式:
(厘米),两者满足关系式: 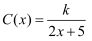 (
( 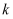 为常数,
为常数, 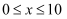 ).若无隔热层,则每年的能源消耗费用为6万元.15年的总维修费用为10万元.记
).若无隔热层,则每年的能源消耗费用为6万元.15年的总维修费用为10万元.记 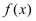 为15年的总费用.(总费用=隔热层的建造成本费用
为15年的总费用.(总费用=隔热层的建造成本费用 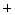 使用15年的能源消耗费用
使用15年的能源消耗费用 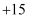 年的总维修费用).
年的总维修费用).
-
(1) 求
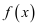 的表达式;
的表达式;
-
(2) 当隔热层的厚度为多少厘米时,
 年的总费用
年的总费用 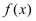 最小?并求
最小?并求 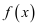 的最小值.
的最小值.
人们用大数据来描述和定义信息时代产生的海量数据,并利用这些数据处理事务和做出决策,某公司通过大数据收集到该公司销售的某电子产品1月至5月的销售量如下表.
月份x | 1 | 2 | 3 | 4 | 5 |
销售量y(万件) | 4.9 | 5.8 | 6.8 | 8.3 | 10.2 |
该公司为了预测未来几个月的销售量,建立了y关于x的回归模型: .
.
参考公式:对于一组数据 , 其回归直线
, 其回归直线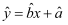 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为 ,
,  .
.
-
(1) 根据所给数据与回归模型,求y关于x的回归方程(
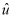 的值精确到0.1);
的值精确到0.1);
-
(2) 已知该公司的月利润z(单位:万元)与x,y的关系为
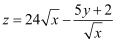 , 根据(1)的结果,问该公司哪一个月的月利润预报值最大?
, 根据(1)的结果,问该公司哪一个月的月利润预报值最大?
已知定义在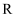 上的函数
上的函数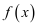 满足
满足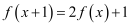 , 当
, 当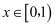 时,
时, . 设
. 设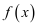 在区间
在区间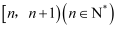 上的最小值为
上的最小值为 . 若存在
. 若存在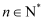 , 使得
, 使得 有解,则实数
有解,则实数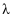 的取值范围是.
的取值范围是.
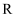 上的函数
上的函数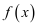 满足
满足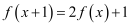 , 当
, 当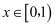 时,
时, . 设
. 设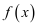 在区间
在区间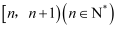 上的最小值为
上的最小值为 . 若存在
. 若存在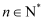 , 使得
, 使得 有解,则实数
有解,则实数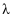 的取值范围是.
的取值范围是.
已知函数 满足关系
满足关系 , 则
, 则 ;
;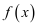 的最大值为.
的最大值为.
 满足关系
满足关系 , 则
, 则 ;
;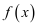 的最大值为.
的最大值为.
最近更新



