勾股定理的证明 知识点题库
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为 ( )
A . 12秒.
B . 16秒.
C . 20秒.
D . 24秒.
如图,在直角梯形ABCD中,AB⊥BC,AE∥DC交BC于E,O是AC的中点,AB= ,
,
AD=2,BC=3,下列结论:①∠CAE=30°;②四边形ADCE是菱形;③;④BO⊥CD,其中
正确结论的个数是( )
A . 4个
B . 3个
C . 2个
D . 1个
如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两边长分别为3和5,则小正方形的面积为

由四个全等的直角三角形组成如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )

A . 1
B . 3
C . 4-2 D . 4+2
D . 4+2
 D . 4+2
D . 4+2
4个全等的直角三角形的直角边分别为a、b,斜边为c.现把它们适当拼合,可以得到如图的图形,利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试.

如图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长是( )

A . 52
B . 42
C . 76
D . 72
中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副”弦图“,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为.

将一根长为17cm的筷子,置于内径为6cm高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为x cm,则x的取值范围是.
如图都是由边长为1的小正方形组成的网格图,小正方形的顶点称为格点.请按下列要求作图.

-
(1) 在图1中,已知线段AB,再作一条端点在格点上的线段CD=
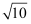 ,并且使CD⊥AB;
,并且使CD⊥AB;
-
(2) 在图2中,已知线段AB,以线段AB为边作一个格点菱形ABCD;
-
(3) 在图3中,作一幅“赵爽弦图”.
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列结论:①x2+y2=49;②x-y=2;③2xy+4=49.其中正确的结论是( )

A . ①②
B . ②
C . ①②③
D . ①③
如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是全等的Rt△ABC和Rt△BED的边长,易知AE=  c,这时我们把关于x的形如ax²+
c,这时我们把关于x的形如ax²+  cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题:
cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题:
 c,这时我们把关于x的形如ax²+
c,这时我们把关于x的形如ax²+  cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题:
cx+b=0的一元二次方程称为“勾系一元二次方程”。请解决下列问题: 
-
(1) 求证:关于x的“勾系一元二次方程”ax²+
 cx+b=0必有实数根;
cx+b=0必有实数根;
-
(2) 若x=-1是“勾系一元二次方程”ax²+
 cx+b=0的一个根,且四边形ACDE的周长是12,求△ABC的面积。
cx+b=0的一个根,且四边形ACDE的周长是12,求△ABC的面积。
2002 年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个能够重合的直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为 1,大正方形的面积为 25,那么直角三角形斜边上的高等于.

教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×  ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
 ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 . 
-
(1) 图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
-
(2) 如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
-
(3) 试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
如图,在△ABC中,∠C=90°,AD是BC边上的中线,DE⊥AB,垂足为E,
求证:AC2=AE2-BE2 .

“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )

A . 4
B . 3
C . 2
D . 1.5
图①是美丽的弦图,包含四个全等的直角三角形.

-
(1) 弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边长为a,较短的直角边长为b,斜边长为c,结合图①,试验证勾股定理;
-
(2) 如图②,将这四个直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,求该飞镖状图案的面积;
-
(3) 如图③,将八个全等的直角三角形紧密拼接,记正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=16,则S2=.
如图所示,我国汉代数学家赵爽,为了证明勾股定理创制了一幅“弦图”,后人称其为“赵爽弦图”(如图),图由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形  、正方形
、正方形  、正方形
、正方形  的面积分别为
的面积分别为  、
、  、
、  .若正方形
.若正方形  的边长为5,则
的边长为5,则  .
.
 、正方形
、正方形 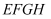 、正方形
、正方形  的面积分别为
的面积分别为 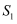 、
、  、
、  .若正方形
.若正方形 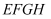 的边长为5,则
的边长为5,则  .
. 
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法如图,火柴盒的一个侧面ABCD(是一个长方形)倒下到AB'C'D'的位置连接AC、AC'、CC',设AB=a ,BC=b,AC=c.

-
(1) 试用a,b有关的代数式表示梯形BCC'D'的面积;
-
(2) 试用a,b,c有关的代数式分别表示△ABC,△AD'C',△AC'C的面积
-
(3) 由(1)和(2)的结论证明勾股定理:
 .
.
我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=10,则S2的值是.

2000多年来,人们对直角三角形三边之间的关系的探究颇感兴趣,古往今来,下至平民百姓,上至帝王总统都愿意探究它,研究它的证明,新的证法不断出现下面给出几种探究方法(由若干个全等的直角三角形拼成以下图形).
试用面积法选择其中一种推导直角三角形的三边a,b,c之间的数量关系.

-
(1) 三边a,b,c之间的数量关系为 .
-
(2) 理由:
最近更新



